НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ МЕТОД

- нахождение искомой функции в виде точной или приближенной линейной комбинации (конечной или бесконечной) известных функций. Указанная линейная комбинация берется с неизвестными коэффициентами, к-рые определяются тем или иным способом из условий рассматриваемой задачи. Обычно для них получается система алгебраич. уравнений.

Классич. примером Н. к. м. является его использование для разложения правильной рациональной дроби в комплексной или действительной области на элементарные дроби. Пусть Р(z) и Q(z) алгебраич. многочлены с комплексными коэффициентами, причем степень пмногочлена Р(z) меньше степени тмногочлена Q(z), коэффициент при старшем члене многочлена Q(z) равен 1, z_i -корень многочлена Q(z)кратности ,

и, следовательно,

Правильная рациональная дробь представима и притом единственным образом в виде

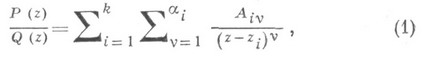
где 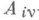- неизвестные пока комплексные числа (их всего т). Для их отыскания обе части равенства приводят к общему знаменателю. После его отбрасывания и приведения в правой части подобных членов получается равенство, в каждой части к-рого стоят многочлены степени не выше чем т- 1: в левой части с известными коэффициентами, в правой - в виде линейных комбинаций неизвестных чисел 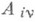. Приравниванием коэффициентов у одинаковых степеней переменного z получается система тлинейных уравнений относительно A _iv, к-рая в силу существования и единственности разложения (1) имеет и притом единственное решение. Иногда бывает удобно использовать несколько иные приемы нахождения коэффициентов 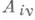. Напр., пусть все корни многочлена 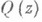простые и, следовательно, разложение (1) имеет вид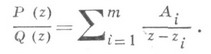

После приведения к общему знаменателю обеих частей и его отбрасывания получается равенство

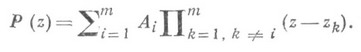
Полагая в нем последовательно сразу получают

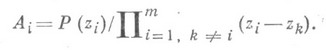
В общем случае бывает полезно комбинировать оба указанных приема нахождения коэффициентов A _iv .

Пусть 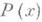и - многочлены с действительными коэффициентами,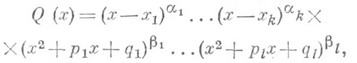

где - действительные корни многочлена 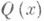соответственно кратностей а квадратный трехчлен 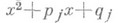с действительными коэффициентами 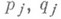является произведением 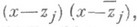где 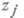- существенно комплексный корень кратности 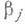, 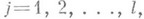многочлена и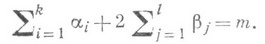

Тогда для правильной рациональной дроби 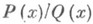существует п притом единственное разложение вида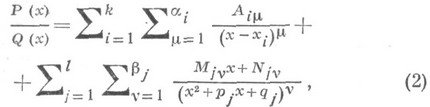

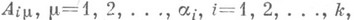
где коэффициенты 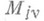и , суть действительные числа. Метод их отыскания тот же, что и в описанном выше комплексном случае: равенство (2) приводится к общему знаменателю, после отбрасывания к-рого приравниваются коэффициенты у одинаковых степеней переменной хв обеих частях равенства. В результате получается система туравнений с тнеизвестными имеющая единственное решение.

Разложение правильных рациональных дробей на элементарные применяется, напр., для разложения рациональных дробей в ряд Лорана (в частности, в ряд Тейлора), для интегрирования рациональных дробей. Н. к. м. используется также при интегрировании рациональных дробей с помощью Остроградского метода, при интегрировании функций вида В этом случае интеграл имеет вид

где степень многочлена Q(х)на единицу меньше степени многочлена Р(х). Для нахождения коэффициентов многочлена Q(х)и числа равенство (3) дифференцируется. После приведения к общему знаменателю и его отбрасывания приравниваются коэффициенты у одинаковых степеней переменной х. В результате снова получается система линейных уравнений с единственным решением. Подобные методы интегрирования могут быть применены и в нек-рых других случаях.

Н. к. м. применяется при отыскании решений дифференциальных уравнений (обыкновенных и с частными производными) в виде степенных рядов. Для этого в окрестности рассматриваемой точки степенной ряд с неопределенными коэффициентами подставляется в данное уравнение. Иногда в результате для коэффициентов ряда получаются соотношения, из к-рых с помощью заданных начальных или граничных условий удается найти эти коэффициенты, а следовательно, и решение уравнения в виде ряда. Напр., решая таким образом гипергеометрическое уравнение, можно получить разложение в ряд гипергеометрической функции.

Н. к. м. применяется и в др. способах решения дифференциальных уравнений, напр. Галеркина методе, Ритца методе, Треффца методе;используется в численных методах: в методе Крылова получения коэффициентов векового уравнения, при приближенном решении интегральных уравнений.

Л. Д. Кудрявцев.