Функции Бесселя — в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где произвольное вещественное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия
НЕЙМАНА РЯД — ряд вида где Бесселя функции (цилиндрич. функции 1 го рода), нек рое число (действительное или комплексное). К. Нейман [1] рассмотрел частный случай, когда целое число. Он показал, что если аналитич. ция в замкнутом круге с центром в начале… … Математическая энциклопедия
НЕЙМАНА МЕТОД ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ — один из методов доверительного оценивания, позволяющий получать интервальные оценки для неизвестных параметров вероятностных законов по результатам наблюдений. Предложен и развит Ю. Нейманом (см. [1], [2]). Суть метода заключается в следующем.… … Математическая энциклопедия
НЕЙМАНА ТЕОРЕМА — эргодическая: для изометрич. оператора в гильбертовом пространстве Ни любого существует предел (понимаемый в смысле сходимости по норме в H). Для непрерывной однопараметрич. группы унитарных преобразований в Ни любогосуществует предел (понимаемый … Математическая энциклопедия
ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ — бесселевы функции, решения Zv дифференциального уравнения Бесселя где v произвольное действительное или комплексное число (см. Бесселя уравнение). Цилиндрические функции произвольного порядка. Если vне является целым числом, то общее решение… … Математическая энциклопедия
Функция Неймана — Функции Бесселя в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где α произвольное действительное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия
Гармонические функции — функции от n переменных (n ≥ 2), непрерывные в некоторой области вместе с частными производными первого и второго порядков и удовлетворяющие в этой области дифференциальному уравнению Лапласа … Большая советская энциклопедия
Бесселевы функции — Функции Бесселя в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где α произвольное действительное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия
Бесселя функции — Функции Бесселя в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где α произвольное действительное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия
Задача Неймана — Задача Неймана, вторая краевая задача в дифференциальных уравнениях краевая задача с заданными граничными условиями для производной искомой функции на границе области так называемые граничные условия второго рода. По типу области… … Википедия
[иногда применяется обозначение 
] могут быть определены через Бесселя функ ции
следующим образом:
. При больших хсправедливо асимптотич. представление
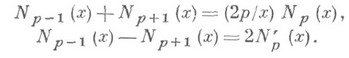
- постоянная Эйлера.
выражаются через тригонометрич. функции, в частности
