- МОРСА ТЕОРИЯ
- общее название для трех различных теорий, основывающихся на идеях М. Морса [1] и описывающих связь алгебро-топологич. свойств топологич. пространства с экстремальными свойствами функций (функционалов) на нем. М. т. является разделом вариационного исчисления в целом;однако последнее шире: напр., оно включает в себя теорию категорий в смысле Люстерннка - Шнирельмана.
1) М. т. критических точек гладких функций f на гладком многообразии М(сокращенно - М. т. 1) разбивается на две части: локальную и глобальную. К локальной части относятся понятия крптич. точки гладкой функции, гессиана функции в ее критич. точке, Морса индекса крптич. точки и т. п. Основным результатом ее является Морса лемма, описывающая строение гладкой функции в окрестности невырожденной критич. точки.
Изучение гладких функций в окрестностях вырожденных точек не относится собственно к М. т. и выделяется в отдельную теорию особенностей дифференцируемых отображений.
Основными утверждениями глобальной М. т. являются следующие. Пусть f - функция на гладком многообразии М. Если множество
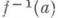 не содержит критич. точек функции f и не пересекается с краем многообразия М, то
не содержит критич. точек функции f и не пересекается с краем многообразия М, то 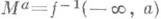 является гладким многообразием с краем
является гладким многообразием с краем 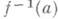 . Если множество
. Если множество 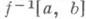 компактно, не пересекается с краем многообразия Ми не содержит критич. точек функции f, то существует такая гладкая изотопия
компактно, не пересекается с краем многообразия Ми не содержит критич. точек функции f, то существует такая гладкая изотопия 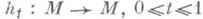 (осуществляемая сдвигом по траекториям градиента функции f), что
(осуществляемая сдвигом по траекториям градиента функции f), что  днффеоморфно отображает
днффеоморфно отображает 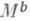 па
па  . В частности,
. В частности, 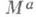 диффеоморфно
диффеоморфно 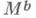 и включение
и включение  является гомотопич. эквивалентностью.
является гомотопич. эквивалентностью.Если множество
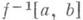 компактно, не пересекается с краем многообразия Ми содержит ровно одну критич. точку
компактно, не пересекается с краем многообразия Ми содержит ровно одну критич. точку 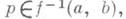 имеющую индекс Морса,
имеющую индекс Морса,  то
то  диффеоморфно многообразию, полученному из
диффеоморфно многообразию, полученному из  приклеиванием ручки индекса
приклеиванием ручки индекса  . В частности, если р- единственная точка глобального минимума функции f, то при малом
. В частности, если р- единственная точка глобального минимума функции f, то при малом  множество
множество 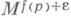 диффеоморфно диску
диффеоморфно диску 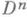 , где
, где 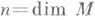 . Отсюда следует, что если М- замкнутое гладкое многообразие, обладающее функцией с ровно двумя критич. точками (причем обе невырожденные), то Мполучается склейкой двух гладких дисков по их общей границе и потому гомеоморфно (но, вообще говоря, не диффеоморфно) сфере
. Отсюда следует, что если М- замкнутое гладкое многообразие, обладающее функцией с ровно двумя критич. точками (причем обе невырожденные), то Мполучается склейкой двух гладких дисков по их общей границе и потому гомеоморфно (но, вообще говоря, не диффеоморфно) сфере 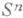
Поскольку приклеивание ручки индекса
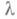 гомотопически эквивалентно приклеиванию клетки размерности
гомотопически эквивалентно приклеиванию клетки размерности 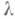 , отсюда непосредственно вытекает следующая основная теорема М. т. 1: каждой Морса функции. f на гладком многообразии М (без края) отвечает гомотопически эквивалентное многообразию М клеточное пространство, клетки к-рого находятся в биективном соответствии с критич. точками функции f, причем размерность клетки равна индексу соответствующей критич. точки. Морса неравенства являются непосредственным следствием этой теоремы. Аналогичная теорема справедлива и для функций Морса триад
, отсюда непосредственно вытекает следующая основная теорема М. т. 1: каждой Морса функции. f на гладком многообразии М (без края) отвечает гомотопически эквивалентное многообразию М клеточное пространство, клетки к-рого находятся в биективном соответствии с критич. точками функции f, причем размерность клетки равна индексу соответствующей критич. точки. Морса неравенства являются непосредственным следствием этой теоремы. Аналогичная теорема справедлива и для функций Морса триад 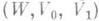
2) М. т. геодезических на римановом многообразии (сокращенно - М. т. 2) описывает гомотопич. тип петель пространства
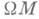 гладкого многообразия Мс римановой метрикой
гладкого многообразия Мс римановой метрикой 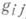 . Ее цель - перенести на случай этого пространства (вернее, его подходящей модели) результаты М. т. 1. Роль функции f играет при этом определенный на пространстве
. Ее цель - перенести на случай этого пространства (вернее, его подходящей модели) результаты М. т. 1. Роль функции f играет при этом определенный на пространстве 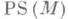 кусочно гладких путей
кусочно гладких путей 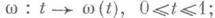 функционал действия Е(иногда неправильно наз. функционалом энергии [5]), значения к-рого на пути
функционал действия Е(иногда неправильно наз. функционалом энергии [5]), значения к-рого на пути 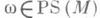 определяются в локальных координатах
определяются в локальных координатах  формулой
формулой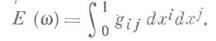
В первоначальном построении М. т. рассматривался функционал длины
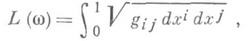
но по многим технич. причинам функционал Еоказывается предпочтительнее. Вместе с тем экстремали функционала
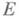 (т. е. пути
(т. е. пути 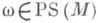 , для к-рых определенный вариацией
, для к-рых определенный вариацией  функционала Елинейный функционал
функционала Елинейный функционал 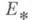 на пространстве
на пространстве 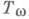 равен нулю) совпадают с геодезическими метрики
равен нулю) совпадают с геодезическими метрики 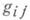 (экстремалями функционала длины L)в их натуральной параметризации.
(экстремалями функционала длины L)в их натуральной параметризации.Пусть р, q- две (не обязательно различные) точки из Ми
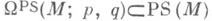 - пространство кусочно гладких путей, соединяющих pc q. Для каждого
- пространство кусочно гладких путей, соединяющих pc q. Для каждого  полагается
полагается
Если риманово многообразие
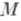 полно, то пространство
полно, то пространство 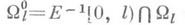 (внутренность множества
(внутренность множества 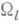 ) деформационно ретрагируется на нек-рое гладкое многообразие В, точками к-рого являются "ломаные геодезические" с фиксированным числом звеньев, соединяющие рс q(так что, в частности, Всодержит все геодезические из
) деформационно ретрагируется на нек-рое гладкое многообразие В, точками к-рого являются "ломаные геодезические" с фиксированным числом звеньев, соединяющие рс q(так что, в частности, Всодержит все геодезические из 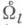 ). При этом функция
). При этом функция 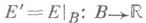 гладкая; для любого
гладкая; для любого  множество
множество  компактно и является деформационным ретрактом множества
компактно и является деформационным ретрактом множества 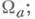 критич. точки функции
критич. точки функции 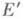 совпадают с экстремалями функционала
совпадают с экстремалями функционала 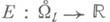 и представляют собой геодезические, соединяющие рс qи имеющие длину
и представляют собой геодезические, соединяющие рс qи имеющие длину 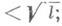 индекс Морса критич. точки функции
индекс Морса критич. точки функции 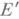 равен индексу Морса соответствующей геодезической; нулевое пространство
равен индексу Морса соответствующей геодезической; нулевое пространство 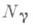 функционала
функционала 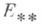 на геодезической
на геодезической 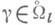 конечномерно и изоморфно нулевому пространству гессиана функции
конечномерно и изоморфно нулевому пространству гессиана функции 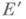 в соответствующей критич. точке; в частности, если ри q не сопряжены ни на одной соединяющей их геодезической
в соответствующей критич. точке; в частности, если ри q не сопряжены ни на одной соединяющей их геодезической 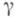 , то
, то 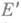 - функция Морса. Применяя М. т. 1 и переходя к пределу при
- функция Морса. Применяя М. т. 1 и переходя к пределу при 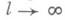 и замечая, что пространство
и замечая, что пространство  гомотопически эквивалентно пространству
гомотопически эквивалентно пространству 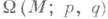 всех непрерывных путей, соединяющих pc q, получаем следующую основную теорему М. т. 2: пусть М- полное риманово многообразие и р, q- две его точки, не сопряженные ни на какой соединяющей их геодезической. Пространство
всех непрерывных путей, соединяющих pc q, получаем следующую основную теорему М. т. 2: пусть М- полное риманово многообразие и р, q- две его точки, не сопряженные ни на какой соединяющей их геодезической. Пространство 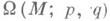 всех путей, соединяющих рс q, гомотопически эквивалентно клеточному пространству, клетки размерности
всех путей, соединяющих рс q, гомотопически эквивалентно клеточному пространству, клетки размерности 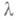 к-рого находятся в биективном соответствии с геодезическими индекса
к-рого находятся в биективном соответствии с геодезическими индекса 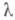 , соединяющими рс q.
, соединяющими рс q.Так как гомотопич. тип пространства
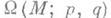 не зависит от выбора точек ри q, то теорема дает, в частности, описание гомотоппч. типа пространства петель
не зависит от выбора точек ри q, то теорема дает, в частности, описание гомотоппч. типа пространства петель 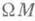
Известно [10], что для нестягиваемого многообразия Мпространство
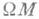 имеет нетривиальные группы гомологии в сколь угодно больших размерностях. В силу основной теоремы М. т. 2 отсюда следует, что несопряженные точки в полном римановом нестягиваемом многообразии соединены бесконечным числом геодезических (на примере сферы видно, что, вообще говоря, эти геодезические могут быть отрезками одной периодической геодезической).
имеет нетривиальные группы гомологии в сколь угодно больших размерностях. В силу основной теоремы М. т. 2 отсюда следует, что несопряженные точки в полном римановом нестягиваемом многообразии соединены бесконечным числом геодезических (на примере сферы видно, что, вообще говоря, эти геодезические могут быть отрезками одной периодической геодезической).В даваемом основной теоремой описании гомотопич. типа фигурируют (хотя и неявно) поля Якоби, поэтому М. т. устанавливает связь между кривизной многообразия и его топологией. Напр., если М- полное односвязное риманово многообразие, кривизна к-рого по всем двумерным направлениям неположительна, то любое поле Якоби, обращающееся в нуль в двух точках геодезической, является тождественно нулевым. Поэтому пространство петель
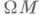 такого многообразия имеет тип нульмерного клеточного пространства и, следовательно (ввиду односвязности М), стягиваемо. Поэтому Мтакже стягиваемо, т. е. гомотопически эквивалентно пространству
такого многообразия имеет тип нульмерного клеточного пространства и, следовательно (ввиду односвязности М), стягиваемо. Поэтому Мтакже стягиваемо, т. е. гомотопически эквивалентно пространству 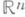 . Более тонкое использование соображений М. т. показывает, что Мдаже диффеоморфно пространству
. Более тонкое использование соображений М. т. показывает, что Мдаже диффеоморфно пространству 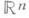 (см. [3], [5]).
(см. [3], [5]).Весьма эффективным оказалось применение М. т. к топологии групп Ли [3]. Напр., для любой односвязной группы Ли G пространство
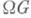 имеет гомотопич. тип клеточного пространства без нечетномерных клеток. Апофеозом здесь является теорема Ботта о периодичности, играющая основополагающую роль в K-теории и, следовательно, во всей дифференциальной топологии. Пусть V- предел последовательности вложенных унитарных групп
имеет гомотопич. тип клеточного пространства без нечетномерных клеток. Апофеозом здесь является теорема Ботта о периодичности, играющая основополагающую роль в K-теории и, следовательно, во всей дифференциальной топологии. Пусть V- предел последовательности вложенных унитарных групп 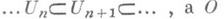 - предел последовательности вложенных ортогональных групп
- предел последовательности вложенных ортогональных групп 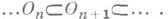 Теорема периодичности Ботта утверждает, что имеют место гомотопич. эквивалентности
Теорема периодичности Ботта утверждает, что имеют место гомотопич. эквивалентности 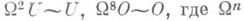 есть n-кратная итерация функтора перехода к пространству петель. Эта теорема позволяет вычислить гомотопич. группы
есть n-кратная итерация функтора перехода к пространству петель. Эта теорема позволяет вычислить гомотопич. группы 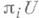 и
и 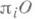 и, следовательно, гомотопич. группы
и, следовательно, гомотопич. группы 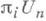 и
и 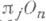 при
при 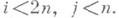
М. т. 2 обобщается также на случай, когда вместо точек р, q рассматриваются гладкие подмногообразия V0 , V1 многообразия М. Изучается функционал действия на пространство
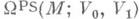 всех кусочно гладких путей
всех кусочно гладких путей 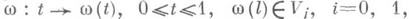 трансверсальных на концах кV0 и V1 , и устанавливается связь экстремалей этого функционала с гомотопич. типом пространства
трансверсальных на концах кV0 и V1 , и устанавливается связь экстремалей этого функционала с гомотопич. типом пространства 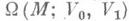 . Соответствующая основная теорема аналогична сформулированной выше основной теореме М. т. 2; трудность состоит в геометрич. интерпретации индекса Морса геодезической.
. Соответствующая основная теорема аналогична сформулированной выше основной теореме М. т. 2; трудность состоит в геометрич. интерпретации индекса Морса геодезической.3) Естественным развитием М. т. 2 является М. т. критич. точек гладких функций на банаховых (бесконечномерных) многообразиях - М. т. 3, представляющая собой уже не аналог, а непосредственное обобщение М. т. 1. К настоящему времени (1982) М. т. 3 находится в стадии становления и построена лишь в весьма предварительном контексте при очень сильных (и явно не необходимых) условиях на модельное банахово пространство (типа сепарабельности и гильбертовости), когда не возникает специфических функционально-аналитич. трудностей [9], хотя имеются и попытки построения М. т. 3 в довольно общей ситуации. Поэтому в современном виде М. т. 3 является почти дословным повторением М. т. 1. Единственное заслуживающее быть отмеченным отличие состоит в том, что в М. т. 3 условие компактности множеств
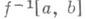 заменяется условием СПале - Смейла (см. Морса функция), к-рое, впрочем, выполняется не во всех интересных ситуациях. Кроме того, хотя для банаховых многообразий приходится приклеивать и ручки бесконечного индекса, в силу гомотопич. тривиальности бесконечномерных сфер эти ручки на гомотопич. тип не влияют. Поэтому в основной теореме М. т. 3 участвуют лишь критич. точки конечного индекса.
заменяется условием СПале - Смейла (см. Морса функция), к-рое, впрочем, выполняется не во всех интересных ситуациях. Кроме того, хотя для банаховых многообразий приходится приклеивать и ручки бесконечного индекса, в силу гомотопич. тривиальности бесконечномерных сфер эти ручки на гомотопич. тип не влияют. Поэтому в основной теореме М. т. 3 участвуют лишь критич. точки конечного индекса.Лит.:[1] Morse M., The calculus of variations in the large, N. Y., 1934; [2] Mилнор Д ж., Теория Морса, пер. с англ., М., 1965; [3] его же, Теорема об h-кобордизме, пер. с англ., М., 1969; [4] 3ейферт Г., Трельфалль В., Вариационное исчисление в целом, пер. с нем., М., 1947; [5] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. снем., М., 1971; [6] Бишоп Р.-Л., Криттенден Р.- Д ж., Геометрия многообразий, пер. с англ., М., 1967; [7] Постников М. М., Введение в теорию Морса, М., 1971; [8] его же, Вариационная теория геодезических, М., 1965; [9] Иллс Д ж., "Успехи матем. наук", 1969, т. 24, в. 3, с. 157- 210; [10] Серр Ж.-П., Сингулярные гомологии расслоенных пространств, в кн.: Расслоенные пространства и их приложения, пер. с франц., М., 1958, с. 9-98.
М. М. Постников, Ю. Б. Рудяк.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
