МИНИМАЛЬНАЯ МОДЕЛЬ

- алгебраическое многообразие с условием минимальности относительно существования бирациональных морфизмов на неособые многообразия. Точнее, пусть В- класс всех бирацио-нально эквивалентных неособых проективных многообразий над алгебраически замкнутым полем k, поля функций к-рых изоморфны заданному конечно порожденному расширению Кнад k. Многообразия из класса Вназ. проективными моделями этого класса, или проективными моделями поля К/k. Многообразие наз. относительно минимальной моделью, если всякий бирациональный морфизм является изоморфизмом. Иначе говоря, относительно М. м.- это минимальные элементы в Вотносительно частичного порядка, определяемого следующим отношением доминирования: Х ₁ доминирует Х ₂ , если существует бирациональный морфизм Если относительно М. м. единственна в В, то она наз. минимальной моделью.

В каждом классе бирационально эквивалентных кривых существует единственная (с точностью до изоморфизма) неособая проективная кривая. Так что всякая неособая проективная кривая является М. м. В общем случае, если класс Вне пуст, то в нем существует хотя бы одна относительно М. м. Непустота класса Визвестна (благодаря теоремам о разрешении особенностей) для многообразий любой размерности в характеристике 0 и для многообразий размерности в характеристике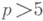

Основные результаты о М. м. алгебраич. поверхностей заключаются в следующих утверждениях.

1) Неособая проективная поверхность Xтогда и только тогда является относительно М. м., когда она не содержит исключительных кривых первого рода (см. Исключительное подмногообразие).

2) Всякая неособая полная поверхность обладает бирациональным морфизмом на относительно М. м.

3) В каждом непустом классе Вбирационально эквивалентных поверхностей, кроме классов рациональных и линейчатых поверхностей, существует (и притом единственная) М. м.

4) Если В- класс линейчатых поверхностей с кривой Срода 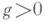в качестве базы, то все относительно М. м. в Висчерпываются геометрически линейчатыми поверхностями

5) Если В- класс рациональных поверхностей, то все относительно М. м. в Висчерпываются проективной плоскостью и серией минимальных рациональных линейчатых поверхностей

для всех целых n>=2.

Имеется (см. [6], [7]) обобщение теории М. м. поверхностей на регулярные двумерные схемы. Описаны (см. [2]) М. м. рациональных поверхностей, определенных над произвольным полем.

О М. м. для многообразий размерности почти ничего не известно (1982).

Лит.:[1] Алгебраические поверхности, М., 1965 (Тр. Матем. ин-та АН СССР, т. 75); [2] Псковских В. А., "Изв. АН СССР. Сер. матем.", 1979, т. 43, № 1, с. 19-43; [3] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972; [4] Bombieri E., Husemoller D., Classification and embeddings of surfaces. Proc. symp. pure math., v. 29 - Algebraic geometry arcata 1974, Rhode Island, 1975, p. 329-420; [5] Hаrtshorne R., Algebraic geometry, N. Y.-Hdlb.-В., 1977; [6] Lichtenbaum S., "Amer. J. Math.", 1968, v. 90, № 2, p. 380-405; [7] Shafarevitch I., Lectures on minimal models and birational transformations of twodimensional schemes, Bombey, 1966. В. А. Псковских.