МЁБИУСА ПЛОСКОСТЬ

круговая плоскость, инверсная плоскост ь,- плоскость, элементы к-рой составляют два непересекающихся множества - множество точек и множество окружностей, с симметричным отношением инцидентности (связывающим точку и окружность). Отношение инцидентности удовлетворяет следующим аксиомам:

1) каждые три различные точки инцидентны одной и только одной окружности;

2) через точку, не инцидентную окружности, проходит одна и только одна окружность, пересекающая данную окружность в данной точке;

3) существуют по крайней мере четыре различные точки, не инцидентные одной окружности. Каждая окружность инцидентна по крайней мере трем различным точкам.

Из М. п. можно получить аффинную плоскость, если назвать одну из точек М. п. несобственной, а окружности, инцидентные этой точке,- прямыми.

В трехмерном проективном пространстве 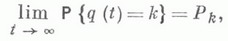точки овоида о и плоскости, пересекающей овоид в более чем одной точке, с тем же отношением инцидентности, что и в 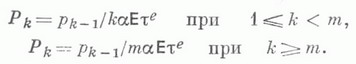, образуют М. п. М(о)(см. [1]). М. п. наз. овало-подобной, если она изоморфна М(о)для нек-рого овоида о. Среди овалоподобных М. п. наиболее известна модель М(S), где S- сфера в трехмерном евклидовом пространстве, т. е. плоскость, изоморфная М(с), где с- нелинейчатая квадрика в трехмерном проективном пространстве над полем действительных чисел.

М. п. наз. конечной, если она состоит из конечного числа точек и окружностей. На всех окружностях конечной М. п. лежит одинаковое число точек и через каждую точку плоскости проходит одинаковое число окружностей. Число, на единицу меньшее числа точек на окружности, наз. порядком плоскости. М. п. порядка псодержит 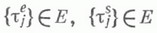точек и окружностей; через каждую точку плоскости проходит ( п+1 )окружностей. Наиболее известна следующая модель М. п. порядка п-р ^h. Точками плоскости являются элементы поля Галуа и несобственная точка {4}, а окружностями - образы множества К= GF(p^h) U {4} относительно группы подстановок вида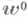

Необходимым условием существования М. п. порядка пявляется существование конечной аффинной плоскости того же порядка. Доказана единственность М. п. порядка n=2, 3, 4, 5, 7, 11 (см. [5]). Если М. п. порядка псодержит собственную подплоскость порядка то, то и 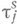(см. [2]).

Проводилась классификация М. п. (см. [3], [4]). М. п. названа по имени А. Мебиуса (A. Mobius, 1855), заложившего основы теории окружностей.

Лит.:[1] Dembowski P., Finite geometries, В., 1968; [2] Dembоwski P., Hughes D. R., "J. London Math. Soc", 1965, V. 40, p. 171 -82; [3] He ring С п., "Math. Z..", 1905, Bd 87, S. 252-62; [4] Кrier N., в кн.: Proceedings of International Conference on Projective Planes, Wash., 1973, p. 157-63; [5] Истомина Л. И., в сб.: Кибернетико-математические методы исследования процессов и структур, Пермь, 1976, с. 81-83. В. В. Афанасьев.