МАКСИМИЗАЦИЯ И МИНИМИЗАЦИЯ ФУНКЦИЙ

конечного числа переменных - задача поиска экстремума функции под этой задачей понимается:

1) нахождение

2) отыскание точек максимума или минимума, если достигаются на допустимом множестве (см. Максимум и минимум функции).

3) построение максимизирующей последовательности {x_i} или мини м и з и р у roll; ей последовательности {х _i} таких, что

если недостижимы на X.

Исследованием экстремумов функций дискретных аргументов занимается дискретное программирование и целочисленное программирование. Ниже освещены только методы М. и м. ф. непрерывных аргументов.

Классические (непрямые) методы М. и м. ф. применимы только для гладких функций. Они используют необходимое условие экстремума для поиска стационарных точек. Нули производных

вычисляются на практике чаще всего одним из многочисленных методов последовательных приближений (см. [3]). С другой стороны, каждую задачу решения конечных функциональных уравнений вида

можно интерпретировать как задачу М. и м. ф., напр. функции

и применить для решения последней один из специфич. методов М. и м. ф.

Прямые методы М. и м. ф. основываются на непосредственном сравнении значений f(x).в двух или нескольких точках.

Для практич. отыскания экстремумов применяются итеративные алгоритмы вида:

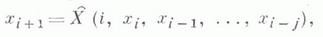
где i - номер итерации, а - нек-рый оператор. При этом обычно предполагается:

1) сходимость алгоритма в том или ином смысле, чаще всего в смысле

2) локальность итерационной процедуры, т. е. алгоритм "помнит" значения хтолько для итераций в нек-рой окрестности текущего положения х;. При получается простой марковский вычислительный процесс без памяти.

Оператор может быть детерминированным в детерминированных методах или содержать стохастич. параметры. В вычислительной практике часто сочетают стохастич. методы с детерминированными, напр. в покоординатного спуска методе направление спуска может определяться случайным образом. Вероятностные характеристики стохастических параметров, в свою очередь, могут меняться от итерации к итерации (поиск с адаптацией и "самообучением", случайный поиск).

Широко применяют и комбинирование различных детерминированных методов, к к-рому относится последовательное и параллельное вычисление экстремума несколькими методами, композиции алгоритмов вида и т. п. Напр., метод Левенберга - Марквардта

к-рый при a_i = 0 совпадает с градиентным методом, а при b_i = 0 с методом Ньютона.

Одномерная оптимизация, то есть М. и м. ф. f(x),помимо самостоятельного интереса, является необходимым этапом большинства применяемых методов. К специфически одномерным относятся, напр., Фибоначчи метод, половинного деления метод (дихотомии метод), парабол метод. Методами М. и м. ф. многих переменных являются градиентный метод, наискорейшего спуска метод, покоординатного спуска метод, симплексный поиск, сканирования метод, сопряженных градиентов метод, тяжелого шарика метод, установления метод и др.

Алгоритмы большинства из перечисленных методов укладываются в схему метода спуска (п о д ъ е м а): причем для всех i (условие релаксации). Они различаются между собой либо выбором вектора направления y_i спуска, либо выбором способов движения вдоль вектора спуска, определяемым шаговым множителем эе.

Овражные методы разработаны для функций, рельеф к-рых имеет вид "оврагов с крутыми склонами" (см. Овражных функций методы минимизации). Ординарные (не овражные) методы, будучи примененными здесь, дают извилистый релаксационный путь, требующий чрезмерно больших затрат машинного времени для вычисления экстремума.

Сравнительная эффективность методов оценивается по многим и противоречивым критериям. Сюда входят: точность решения, скорость решения, надежность метода, время подготовки задачи к счету, сходимость алгоритма и др. Область применения каждого из апробированных методов весьма ограничена.

Для испытания методов разработаны наборы стандартных тест-функций, характерных для различных функциональных классов (см. [1]). Усиленно исследуется сходимость методов М. и м. ф. (см. [6], [8]). Однако сходимость - это качество, к-рое не является ни необходимым, ни достаточным для эффективного окончания вычислений.

Все перечисленные выше методы приводят к одному из локальных экстремумов, если начальное приближение принадлежит области притяжения точки этого экстремума. Нахождение глобального экстремума гарантируется лишь для выпуклых и родственных им унимодальных функций. Теория отыскания глобального экстремума находится (1982) в начальной стадии развития (см. Многоэкстремальная задача). Другим развивающимся направлением М. и м. ф. является оптимизация негладких функций (см. [4], [13], [16]). В частности, к негладкой функции, как правило, приводит задача минимизации функции максимума (см. Максимин;численные методы). По-видимому, все из общеупотребительных методов оптимизации имеют содержательный физический, экономический или биологический смысл.

Соответствующие исследования только разворачиваются (см. [9]) и приводят к созданию новых методов (см. также Непрерывные аналоги итерационных методов). Если значения исследуемой функции определяются статистически со стохастич. помехой, то для отыскания экстремума применяется один из методов стохастической аппроксимации. Сюда же примыкает и планирование эксперимента.

Экспериментальные методы М. и м. ф. используют воспроизведение различных физич. процессов для поиска экстремумов. К ним относится и моделирование на АВМ (см. [17]). Несмотря на удобство и дешевизну использования в простейших автоматич. оптимизаторах, последнее не обеспечивает высокой точности вычисления.

Графи ч. методы пригодны только для прикидочных расчетов и построения начального приближения для итеративных методов.

Если допустимое множество задано в виде функциональных условий

(связи и ограничения, условный экстремум), то для поиска экстремумов применяются методы математич. программирования. Эта же задача может быть сведена к последовательности задач на безусловный экстремум с помощью штрафных и барьерных функций (см. Штрафных функций метод).

Лит.:[1] А о к и М., Введение в методы оптимизации, пер. с англ., М., 1977; [2] Б а х в а л о в Н. С., Численные методы, 2 изд., М., 1975; [3] Березин И. С., Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966; 2 изд., т. 2. М., 1962; [4] Васильев Ф. П., Лекции по методам решения экстремальных задач, М., 1974; [5] Г у п а л А. М., Стохастические методы решения негладких экстремальных задач, К., 1979; [6] Карманов В. Г., Математическое программирование, М., 1975; [7] М о и с е е в Н. Н., Иванилов Ю. П., Столярова Е. М., Методы оптимизации, М., 1978; [8] Пшеничный Б. Н., Данилин Ю. М., Численные методы в экстремальных задачах, М., 1975; [9] Разумихин Б. С., Физические модели и методы теории равновесия в программировании и экономике, М., 1975; [10] Р а с т р и г и н Л. А., Системы экстремального управления, М., 1974; [11] Саульев В. К., Самойлова И. И., в сб.: Итоги науки и техники. Математический анализ, т. 11, М., 1973, с. 91 - 128; [12] Уайлд Д.-Дж., Методы поиска экстремума, пер. с англ., М., 1967; [13] Федоров В. В., Численные методы максимина, М., 1979; [14] О р т е г а Д., Рейнболдт В., Итерационные методы решения нелинейных систем уравнений со многими неизвестными, пер. с англ., М., 1975; [15] Современное состояние теории исследования операций, М., 1979; [16] Nonsmooth Optimization, Oxf., 1978; [17] Towards Global Optimisation, v. 1-2, Amst.- N. Y., 1975-78; [18] Евтушенко Ю. Г., "Ж. вычисл. матем. и матем. физ.", 1971, т. II, № 6, с. 1390-1403.

Ю. П. Иванилов, В. В. Охрименко.