ФИБОНАЧЧИ МЕТОД

- разновидность одномерного поиска экстремума функции путем последовательного сужения интервала неопределенности. Единственное ограничение, налагаемое на исследуемую функцию 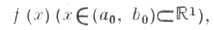- требование строгой унимодальности на заданном интервале.
При последовательном сужении значения f(х)вычисляются (или замеряются) в заранее ограниченном числе . пробных точек. В результате получается последовательность сужающихся интервалов неопределенности, содержащих искомый экстремум:

Чтобы сузить интервал неопределенности для произвольной строго унимодальной функции, нужно знать не менее двух ее пробных значений. В Ф. <м. внутри каждого текущего интервала неопределенности (a_i, b_i) подбираются ровно две пробные точки симметрично от середины интервала. Далее, от одной из пробных точек отбрасывается конец интервала с наихудшими значениями f(х). Получается ( а _i+1 , b_i+1), где в дополнение к оставшейся старой пробной точке симметрично строится новая. Отсюда для длин интервалов 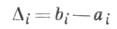следует рекуррентное уравнение
(Помимо прочего выше предполагалось, что выполнено условие перекрывания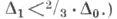
Решение уравнения при условии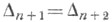 дает где -Фибоначчи числа.
Точка экстремума
В простейшем варианте Ф. м. (когда предполагается, что пробные точки и пробные значения f(х)определяются абсолютно точно), чтобы сузить исходный интервал неопределенности с до надо взять число ппробных точек из неравенства С учетом поправок на точность определения значений функции вышеприведенная оценка несколько усложняется.
Существует предел

Это дает основание ввеси метод золотого сечения- такой вариант Ф. <м., где т. е. пробные точки осуществляют золотое сечение текущего интервала. Преимущество последнего метода заключается в том, что число пробных точек заранее не планируется.
Разработаны модификации Ф. м. для нефинитных функций, для сокращения вычислении при равенстве f(x) в двух пробных точках, для повышения устойчивости счета и др.
Ф. м. значительно превосходит по эффективности дихотомию (см. Половинного деления метод). Однако для оптимизации дифференцируемых функций Ф. м. малоцелесообразен (см. Спуска метод, Максимизация и минимизация функции).

Лит.:[1] Kiefer J., лProc. Amer. Math. Soc.