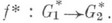ЛОКАЛЬНО НИЛЬПОТЕНТНАЯ ГРУППА
- ЛОКАЛЬНО НИЛЬПОТЕНТНАЯ ГРУППА
группа, каждая конечно порожденная подгруппа к-рой нильпотентна (см. Нильпотентная группа). В Л. н. г. все элементы конечного порядка образуют нормальную подгруппу, являющуюся периодич. частью этой группы. Эта подгруппа разлагается в прямое произведение силовских подгрупп, а факторгруппа по ней не имеет кручения. Л. н. г. без кручения обладает свойством однозначности извлечения корня: если для элементов аи bпри каком-либо целом 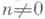 будет а п=b п, то а=b. Каждая Л. н. г. Gбез кручения обладает Мальцев^ с к и м пополнением, т. е. вкладывается в однозначно определенную Л. н. г. без кручения G* такую, что в ней разрешимы все уравнения вида xn = g, где
будет а п=b п, то а=b. Каждая Л. н. г. Gбез кручения обладает Мальцев^ с к и м пополнением, т. е. вкладывается в однозначно определенную Л. н. г. без кручения G* такую, что в ней разрешимы все уравнения вида xn = g, где 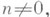 a g - любой элемент из G. Это пополнение функториально, т. е. любой гомоморфизм
a g - любой элемент из G. Это пополнение функториально, т. е. любой гомоморфизм 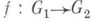 Л. н. г. без кручения G1 в G2 однозначно продолжается до гомоморфизма
Л. н. г. без кручения G1 в G2 однозначно продолжается до гомоморфизма 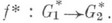
Лит.:[1] . К у р о ш А. Г., Теория групп, 3 изд., М., 1967; [2] Каргаполов М. И., Мерзляков Ю. И., Основы теории групп, 2 изд., М., 1977. А. Л. Шмелъкин.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "ЛОКАЛЬНО НИЛЬПОТЕНТНАЯ ГРУППА" в других словарях:
НИЛЬПОТЕНТНАЯ ГРУППА — группа, обладающая нормальным рядом таким, что каждый его фактор лежит в центре факторгруппы (такой ряд наз. центральным). Длина наиболее короткого центрального ряда Н. г. наз. ее классом (или ступенью) нильпотентности. В любой Н. г. нижний (а… … Математическая энциклопедия
ОБОБЩЕННО НИЛЬПОТЕНТНАЯ ГРУППА — группа одного из обобщенно нильпотентных классов групп. Класс групп наз. обобщенно нильпотентным, если он содержит все нильпотентные группы и пересекается с классом конечных групп по классу всех конечных нильпотентных групп. Рассматривалось… … Математическая энциклопедия
ЭНГЕЛЕВА ГРУППА — группа G, в к рой для любых двух элементов существует такое целое п=п( а, b), что [[. . .[[a, b], b], . ..], b] = 1, где [ а, b] коммутатор элементов a и b. Если это число пможно выбрать не зависящим от а, b, то G наз. Э. г. конечного класса п.… … Математическая энциклопедия
Конечно определенная группа — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Конечно определённая группа — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Конечнопорожденная группа — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Конечнопорождённая группа — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Метациклическая группа — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Мультипликативная группа поля — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Периодическая группа — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
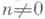 будет а п=b п, то а=b. Каждая Л. н. г. Gбез кручения обладает Мальцев^ с к и м пополнением, т. е. вкладывается в однозначно определенную Л. н. г. без кручения G* такую, что в ней разрешимы все уравнения вида xn = g, где
будет а п=b п, то а=b. Каждая Л. н. г. Gбез кручения обладает Мальцев^ с к и м пополнением, т. е. вкладывается в однозначно определенную Л. н. г. без кручения G* такую, что в ней разрешимы все уравнения вида xn = g, где 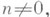 a g - любой элемент из G. Это пополнение функториально, т. е. любой гомоморфизм
a g - любой элемент из G. Это пополнение функториально, т. е. любой гомоморфизм 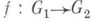 Л. н. г. без кручения G1 в G2 однозначно продолжается до гомоморфизма
Л. н. г. без кручения G1 в G2 однозначно продолжается до гомоморфизма