ЛИ НИЛЬАЛГЕБРА

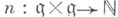- алгебра Ли над полем k, определяемая наличием функции такой, что 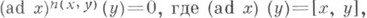для любых х,. Основной вопрос о Лин.- условия на 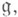k, п, при к-рых (локально) нильпотентна (см. Ли нильпотентная алгебра). Конечномерная над kЛи н.- нильпотентна. С другой стороны, над любым полем существуют конечно порожденные ненильпотентные Ли н. [1]. Пусть п - константа. Ли н. локально нильпотентна, если chark=0 или если где p = chark > 0 (теорема Кострикина [2]). Локальная нильпотентность имеет место и в случае, когда локально разрешима. Бесконечно порожденная Ли н. ненильпо-тентна при (см. [3]), а при ненильпотентность сохраняется и при условии разрешимости. Неизвестно (1982), нильпотентны ли Ли н., если char k=0 (при ответ положительный). Открыт (1982) вопрос о локальной нильпотентности Ли н. при n>р+1. Изучение Ли н. над полем k,char k=p>0, тесно связано с Вёрнсайда проблемой.

Лит.:[1] Г о л о д Е. С., "Изв. АН СССР. Сер. матем.", 1964, т. 28, № 2, с. 273-76; [2] К о с т р и к и н А. И., "Изв. АН СССР. Сер. матем.", 1959, т. 23, № 1, с. 3-34; [3] Размыслов Ю. П., Алгебра и логика, 1971, т. 10, № 1, с. 33- 44; [4] Б а х т у р и н Ю. A., Lectures on Lie algebras. В., 1978; [5] Braun A., "J. Algebra", 1974, v.31, p. 287-92.

Ю. А. Бахтурин.