КРАТНО КРУГОВАЯ ОБЛАСТЬ

КРАТНО КРУГОВАЯ ОБЛАСТЬ

область Рейнхарт а,- область Dкомплексного пространства с центром в точке такая, что вместе с каждой точкой ей принадлежат и все точки вид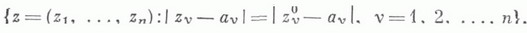

К. к. ,о. Dс а=0 инвариантна относительно преобразований 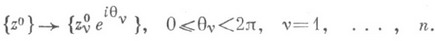К. к. о. составляют подкласс Гартогса областей и подкласс класса круговых областей, определяемых условием: вместе с каждой точкой они содержат и все точки вида 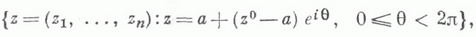т. е. все точки окружности с центром а и радиусом расположенной на комплексной прямой, проходящей через аи z0.

К. к. о. Dпаз. полной кратно круговой областью, если вместе с каждой точкой 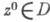ей принадлежит поликруг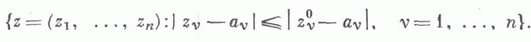

Полная К. к. о. звездообразна относительно ее центра а. Примеры полных К. к. о.: шары и поликруги в 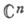Круговая область Dназ. полной круговой областью, если вместе с каждой точкой она содержит и весь круг

К. к. о. Dназ. логарифмически выпуклой кратно круговой областью, если образ 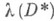множества при отображении является выпуклым множеством в действительном пространстве Важное свойство логарифмически выпуклых полныхК. к. о. <состоит в том, что каждая такая область в есть внутренность множества точек абсолютной сходимости (т. е. область сходимости) нек-рого степенного ряда по переменным 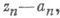и обратно: область сходимости любого степенного ряда по есть логарифмически выпуклая полная К. к. о. с центром а=0.

Лит.:[1] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; [2] Шабат Б. В., Введение в комплексный анализ, 2 изд., М-, 1976. Е. Д. Соломенцев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужна курсовая?

Полезное


Смотреть что такое "КРАТНО КРУГОВАЯ ОБЛАСТЬ" в других словарях:

  • СТЕПЕННОЙ РЯД — 1)С. р. по одному комплексному переменному z функциональный ряд вида где a центр ряда, bk его коэффициенты, bk(z a)k члены ряда. Существует число r, называемое радиусом сходимости С. р. (1) и определяемое по формуле Коши Адамара такое, что при |z …   Математическая энциклопедия

  • ПОЛИКРУГ — полицилиндр, область комплексного пространства , являющаяся топологич. произведением n кругов, Точка центр поликруга Д, r=(r1, . . ., rn), rv >0, v=l, . . ., n, его мультирадиус. При а=0, r=(1, . . ., 1) получается единичный поликруг. Остовом… …   Математическая энциклопедия

  • КРУГ СХОДИМОСТИ — степенного ряда круг вида в к ром ряд (1) абсолютно сходится, а вне его, при расходится. Иными словами, К. с. есть внутренность множества точек сходимости ряда (1). Радиус RК. с. наз. радиусом сходимости ряда (1). К. с. может вырождаться в точку… …   Математическая энциклопедия

  • КВАНТОВАЯ МЕХАНИКА — (волновая механика), теория, устанавливающая способ описания и законы движения микрочастиц (элем. ч ц, атомов, молекул, ат. ядер) и их систем (напр., кристаллов), а также связь величин, характеризующих ч цы и системы, с физ. величинами,… …   Физическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»