КОШИ - АДАМАРА ТЕОРЕМА

КОШИ - АДАМАРА ТЕОРЕМА

пусть задан степенной ряд

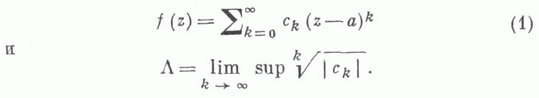
Если то ряд (1) сходится только в точке z=a; если то ряд (1) абсолютно сходится в круге радиуса

и расходится вне этого круга при если то ряд (1) абсолютно сходится при всех Содержание К. - А. т. выражается, таким образом, формулой Коши - Адамара (2), к-рую при этом следует понимать в расширенном смысле, включая равенства Иначе говоря, содержание К.- А. т. состоит в том, что внутренность множества точек (абсолютной) сходимости ряда (1) есть круг радиуса (2). В случае действительного степенного ряда (1) формула (2) определяет радиус интервала сходимости В основном К.- А. т. была высказана О. Коши (A. Cauchy) в его лекциях [1], опубликованных в 1821, полную ясность в формулировку и доказательство внес Ж. Адамар [2]. Для степенных рядов

но n комплексным переменным обобщением формулы Коши - Адамара является следующее соотношение:

к-рому удовлетворяют сопряженные радиусы сходимости r1 . . . , rn ряда (3) (см. Круг сходимости). Записав соотношение (4) в виде получают уравнение, определяющее границу нек-рой логарифмически выпуклой кратно круговой области с центром а, к-рая и является внутренностью множества точек абсолютной сходимости ряда (3) при n>1.

Лит.:[1] К о ш и О. Л., Алгебраический анализ, пер. с франц., Лейпциг, 1864; [2] Н a d a m a r d J., "J. math, pures et appl." (4), 18Я2, t. 8, p. 101-86; [3]Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [4] Ш а б а т Б. В., Введение в комплексный анализ, 2 изд., М., 1976.

Е. Д. Соломенцев.



Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужен реферат?

Полезное


Смотреть что такое "КОШИ - АДАМАРА ТЕОРЕМА" в других словарях:

  • Коши - Адамара теорема —         теорема теории аналитических функций, позволяющая судить о сходимости степенного ряда          a0+a1(z z0)+...+an (z z0) n+...,         где a0, a1,..., an фиксированные комплексные числа, a z комплексное переменное. К. А. т. гласит: если… …   Большая советская энциклопедия

  • Формула Коши-Адамара — Основная статья: Степенной ряд Круг сходимости степенного ряда круг вида D = {z: | z − z0 | < R}, , в котором ряд абсолютно сходится, а вне его, при | z − z0 | > R, расходится. Иными словами, круг сходимости степенного ряда есть… …   Википедия

  • Формула Коши — Адамара — Основная статья: Степенной ряд Круг сходимости степенного ряда круг вида D = {z: | z − z0 | < R}, , в котором ряд абсолютно сходится, а вне его, при | z − z0 | > R, расходится. Иными словами, круг сходимости степенного ряда есть… …   Википедия

  • Коши Огюстен Луи — Коши (Cauchy) Огюстен Луи (21.8.1789, Париж, ≈ 23.5.1857, Со), французский математик, член Парижской АН (1816). Окончил Политехническую школу (1807) и Школу мостов и дорог (1810) в Париже. В 1810≈13 работал инженером в г. Шербур. В 1816≈30… …   Большая советская энциклопедия

  • Коши — (Cauchy)         Огюстен Луи (21.8.1789, Париж, 23.5.1857, Со), французский математик, член Парижской АН (1816). Окончил Политехническую школу (1807) и Школу мостов и дорог (1810) в Париже. В 1810 13 работал инженером в г. Шербур. В 1816 30… …   Большая советская энциклопедия

  • КОШИ НЕРАВЕНСТВО — 1) К. н. неравенство для конечных сумм, имеющее вид:.. Доказано О. Коши (A. Cauchy, ;1821); интегральный аналог Буняковского неравенство. 2) К. н. неравенство для модуля производной регулярной аналитич. функции в фиксированной точке акомплексной… …   Математическая энциклопедия

  • КРУГ СХОДИМОСТИ — степенного ряда круг вида в к ром ряд (1) абсолютно сходится, а вне его, при расходится. Иными словами, К. с. есть внутренность множества точек сходимости ряда (1). Радиус RК. с. наз. радиусом сходимости ряда (1). К. с. может вырождаться в точку… …   Математическая энциклопедия

  • Целая функция —         функция, аналитическая во всей плоскости комплексного переменного (см. Аналитические функции). Примерами Ц. ф. могут служить алгебраический многочлен a0 + a1z +... + anzn, функции sinz, cosz, ez. Бесконечно удалённая точка является,… …   Большая советская энциклопедия

  • СТЕПЕННОЙ РЯД — 1)С. р. по одному комплексному переменному z функциональный ряд вида где a центр ряда, bk его коэффициенты, bk(z a)k члены ряда. Существует число r, называемое радиусом сходимости С. р. (1) и определяемое по формуле Коши Адамара такое, что при |z …   Математическая энциклопедия

  • Адамар, Жак — Жак Саломон Адамар фр. Jacques Salomon Hadamard Дата рождения …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»