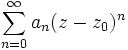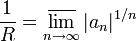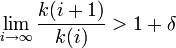Формула Коши — Адамара

Основная статья: Степенной ряд

Круг сходимости степенного ряда

$\sum_{n=0}^\infty a_n(z-z_0)^n$

— круг вида

D = {z: | z − z₀ | < R}, $z\in\mathbb C$,

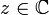в котором ряд абсолютно сходится, а вне его, при | z − z₀ | > R, расходится. Иными словами, круг сходимости степенного ряда есть внутренность множества точек сходимости ряда. Радиус круга сходимости называется радиусом сходимости ряда. Круг сходимости может вырождаться в пустое множество, когда R = 0, и может совпадать со всей плоскостью переменного z, когда $R = \infty$.

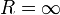Радиус сходимости

Радиус круга сходимости называется радиусом сходимости ряда.

Радиус сходимости ряда Тейлора аналитической функции равен расстоянию от центра ряда до множества особых точек функции, и может быть вычислен по формуле Коши — Адамара:

${1\over R} = {\varlimsup\limits_{n\rightarrow \infty}} \, |a_n|^{1/n}$

Эта формула выводится на основе признака Коши.

Теорема Адамара

Основная статья: :en:Ostrowski-Hadamard gap theorem‎

Для степенного ряда

$f(z)=\sum_{k=0}^\infty \alpha_k (z-z_0)^k$,

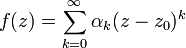у которого почти все коэффициенты равны нулю, в том смысле, что последовательность ненулевых коэффициентов a_k(i) удовлетворяет

$\lim_{i\to\infty} \frac{k(i+1)}{k(i)} &amp;gt; 1 + \delta \,$

для некоторого фиксированного δ > 0, круг с центром z₀ и радиусом, равным радиусу сходимости, является естественной границей — аналитическое продолжение функции, определяемой таким рядом, невозможно за пределы круга.

См. также

• Аналитическое продолжение