КОШИ ОПЕРАТОР

системы обыкновенных дифференциальных уравнений

- зависящий от параметров оператор сопоставляющий значению всякого решения x(t).системы (1) в точке 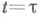значение этого же решения в точке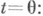

Если система (1) линейная, т. е.

где 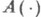-суммируемое на каждом отрезке отображение (или 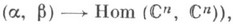то К. о. при всяких есть невырожденное линейное отображение (соответственно ), удовлетворяющее при всяких равенствам:

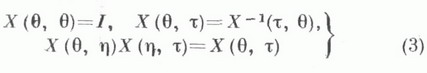
н неравенству

(Для нелинейной системы (1), удовлетворяющей условиям теоремы существования и единственности решения задачи Коши, равенства (3) тоже верны, с должными оговорками относительно областей определения входящих в них операторов.) Общее решение системы

где 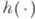- суммируемое на каждом отрезке отображение записывается через К. о. системы (2) формулой произвольных постоянных вариации:

Для К. о. системы (2) имеет место Лиувилля-Остроградского формула

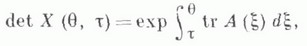
где - след оператора

Производная К. о. системы (1) в точке равна К. о. системы уравнений в вариациях вдоль решения x(t).системы (1), равного хпри 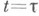(предполагается, что график решения х(t).при всех t, принадлежащих отрезку с концами содержится в области такой, что f - непрерывное отображение имеющее непрерывную в G производную 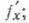это - одна из формулировок теоремы о дифференцируем ости решения по начальному значению).

Для линейной системы (2) с постоянными коэффициентами (A(t)=A) К. о. задается формулой

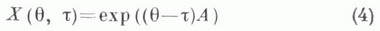
(ехр Вдля линейного оператора Вопределяется как при другом подходе за определение ехр А можно принять формулу (4), положив в ней 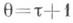). Из формулы (4) видно, что К. о. зависит только от разности параметров

Это равенство - следствие автономности системы, имеющее место для всякой автономной системы

обозначив для системы (5) К. о. через 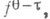получают из формул (3) следующие формулы:

(см. также Динамическая система, Действие группы). Для линейной системы (2) с периодическими коэффициентами:

при нек-ром T>0 и всех - выполняется тождество 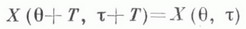при всех _ для такой системы оператор где - любое, наз. оператором м о н о д р о м и и. Матрица, задающая оператор (или, напр., Х( Т,0)) в каком-либо базисе, наз. монодромии матрицей. Все операторы монодромии фиксированной линейной системы с периодическими коэффициентами подобны друг другу:

поэтому спектр оператора монодромии не зависит от т. Собственные значения оператора монодромии наз. мультипликаторами такой системы, через них выражаются условия устойчивости и условной устойчивости системы (см. Ляпунова характеристический показатель, Устойчивость по Ляпунову, Устойчивости теория). Для систем (2) с периодическими комплексными коэффициентами:

для нек-рого T>0 и всех - имеет место теорема Ляпунова:

где при любых является невырожденным линейным оператором 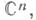периодически зависящим от

Иногда К. о. наз. по-другому (напр., "матрицантом"- для линейной системы, или "оператором сдвига по траекториям"). В. М. Миллионщиков.