КОДАИРЫ ТЕОРЕМА

КОДАИРЫ ТЕОРЕМА

об обращении в нуль, теорема Кодаиры об исчезновении,- теорема о равенстве нулю групп когомологий 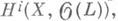i<dim X, где - пучок голоморфных сечений отрицательного векторного расслоения L ранга 1 на компактном комплексном многообразии X. Эквивалентная формулировка К. т. состоит в том, что

для любого положительного векторного расслоения ранга 1 (здесь К X обозначает каноническое линейное расслоение на X). В терминах дивизоров К. т. формулируется как равенство Н'( Х, О X(-D)) = 0 для i<dim Xи любого дивизора Dтакого, что для некоторого nD является гиперплоскнм сечением в каком-либо проективном вложении многообразия X.

К. т. была доказана трансцендентными методами К. Коданрой [1] (см. также [2]) как обобщение на случай произвольной размерности классич. теоремы о регулярности присоединенной системы на алгебраич. поверхности. Существует пример нормальной алгебраич. поверхности над полем положительной характеристики, для к-рой К. т. неверна [4]. Неизвестно (1978), справедлива ли К. т. для неособого алгебраич. многообразия над полем положительной характеристики.

К. т. справедлива и для голоморфных векторных расслоений произвольного ранга, отрицательных в смысле Накано. Обобщением К. т. является также следующий результат:

где L- слабо положительное векторное расслоение ранга r на компактном комплексном многообразии X, - пучок голоморфных форм степени рсо значениями в L. Для слабо отрицательных векторных расслоений Lобращение в 0 имеет место при 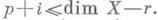Аналоги этих теорем получены для слабо 1-полных многообразий X, т. е. многообразий, допускающих гладкую плюрисубгармонич. функцию y такую, что множества y(x)<с} относительно компактны в Xдля всех cОR, и для компактных комплексных пространств X, обладающих n=dim Xалгебраически независимыми мероморфными функциями [5].

Лит.:[1] Коdairа К., "Proc. Nat. Acad. Sci. USA", 1953, v. 39, p. 1268-73; [2] Уэллс Р., Дифференциальное исчисление на комплексных многообразных, М., 1976; [3] Мumford D., "Amer. J. Math.", 1967, v. 89, № 1, p. 94-104; [4] Zariski O., Algebraic surfaces, B.- Hdlb.-N. Y., 1971; [5] Итоги науки. Алгебра. Топология. Геометрия, т. 15, М., 1977, с. 93-171.

И. В. Долгачев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать курсовую

Полезное


Смотреть что такое "КОДАИРЫ ТЕОРЕМА" в других словарях:

  • СХЕМА — окольцованное пространство, локально изоморфное аффинной схеме. Подробнее, С. состоит из топологич. пространстна X (базисного пространства схемы) и пучка коммутативных колец с единицей на Х (структурного пучка схемы); при этом должно существовать …   Математическая энциклопедия

  • КОГЕРЕНТНЫЙ АНАЛИТИЧЕСКИЙ ПУЧОК — когерентный пучок модулей на аналитическом пространстве Пространство наз. когерентным, если когерентный пучок колец. Любое аналитич. ространство над алгебраически замкнутым полем когерентно. Важнейшими примерами К. а. п. на таком пространстве… …   Математическая энциклопедия

  • КЭЛЕРОВО МНОГООБРАЗИЕ — комплексное многообразие, на к ром можно ввести Кэлера метрику. Иногда такие многообразия на …   Математическая энциклопедия

  • ОСОБЕННОСТИ ДИФФЕРЕНЦИРУЕМЫХ ОТОБРАЖЕНИЙ — раздел математич. анализа и дифференциальной геометрии, в к ром изучаются свойства отображений, сохраняющихся при заменах координат в образе и прообразе отображения (или при заменах, сохраняющих нек рые дополнительные структуры); предлагается… …   Математическая энциклопедия

  • ОСНОВНОГО ТИПА АЛГЕБРАИЧЕСКАЯ ПОВЕРХНОСТЬ — общего типа алгебраическая поверхность, поверхность одного из самых обширных классов алгебраических поверхностей в классификации Энрикеса. А именно, гладкая проективная поверхность Xнад алгебраически замкнутым Полем k наз. О. т. а. п., если где… …   Математическая энциклопедия

  • НОРМАЛЬНОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО — аналитическое пространство, локальные кольца всех точек к рого нормальны, т. е. являются цело вамкнутыми областями целостности. Точка ханалитич. пространства Xназ. нормальной (говорят также, что Xнормально в точке х), если локальное кольцо… …   Математическая энциклопедия

  • ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ — в дифференциальной геометрии поверхность, образованная движением прямой линии. Прямые, принадлежащие этой поверхности, называются прямолинейными образующими, а каждая кривая, пересекающая все прямолинейные образующие, направляющей кривой. Если… …   Математическая энциклопедия

  • ХОДЖА МНОГООБРАЗИЕ — комплексное многообразие, на к ром можно задать метрику Ходжа, т. е. Кэлера метрику, фундаментальная форма к рой определяет целочисленный класс когомологий. Компактное комплексное многообразие является X. м. тогда и только тогда, когда оно… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»