- КОГОМОЛОГИИ
- термин, употребляемый по отношению к функторам гомологической природы, которые, в отличие от гомологии, как правило, контравариантно зависят от объектов основной категории, на которой они определены. В отличие от гомологии, связывающие гомоморфизмы в когомологической точной последовательности повышают размерность. В типичных ситуациях когомологии возникают одновременно с соответствующими гомологиями.
Е. Г. Скляренко.
Когомологии топологического пространства - градуированная группа

которая ставится в соответствие топологич. пространству и абелевой группе G. Понятие К. двойственно понятию гомологии (см. Гомологии теория, Гомологии группа, Александрова- Чеха гомологии и когомологии). Если G- кольцо, то в группе Н*(X, G )определено естественное умножение (произведение Колмогорова - Алекса н дера или U-п роизведение), превращающее эту группу в градуированное кольцо (кольцокогомологий). В случае, когда X- дифференцируемое многообразие, кольцо когомологий Н*(X, R )может быть вычислено при помощи дифференциальных форм на X(см. де Рама теорема).
Когомологий со значениями в пучке абелевых групп - обобщение обычных когомологий топологич. пространств. Имеются две теории когомологий со значениями (или с коэффициентами) в пучках абелевых групп: когомологий Чеха и когомологий Гротендика.
Когомологий Чеха. Пусть X- топологич. пространство,
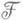 - пучок абелевых групп на X,
- пучок абелевых групп на X, - открытое покрытие пространства X.n-мерной коцепью покрытия
- открытое покрытие пространства X.n-мерной коцепью покрытия  наз. отображение f, к-рое всякому упорядоченному набору
наз. отображение f, к-рое всякому упорядоченному набору 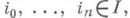 такому, что
такому, что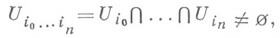
сопоставляет сечение fi0...in пучка Fнад Ui0...in . Множество всех re-мерных коцепей
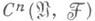 является абелевой группой относительно сложения. Кограничный оператор
является абелевой группой относительно сложения. Кограничный оператор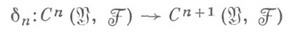
определяется следующим образом:

где символ
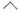 означает, что соответствующий индекс опускается.
означает, что соответствующий индекс опускается.Последовательность

является комплексом (комплекс Чеха). Когомологий этого комплекса обозначаются
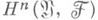 и наз. когомологиями Чеха покрытия
и наз. когомологиями Чеха покрытия  со значениями в
со значениями в  Группа
Группа  совпадает с группой
совпадает с группой  сечений пучка F. При вычислении этих когомологий комплекс Чеха можно заменить его подкомплексом, состоящим из альтернированных коцепей, т. е. коцепей, меняющих знак при перестановке двух индексов и равных 0 в случае, когда два индекса совпадают.
сечений пучка F. При вычислении этих когомологий комплекс Чеха можно заменить его подкомплексом, состоящим из альтернированных коцепей, т. е. коцепей, меняющих знак при перестановке двух индексов и равных 0 в случае, когда два индекса совпадают.Если покрытие
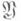 вписано в
вписано в  т. е. для каждого
т. е. для каждого  указано
указано  так, что
так, что  то определен канонический гомоморфизм Н п
то определен канонический гомоморфизм Н п Н п (
Н п (
 ), не зависящий от вписывания т. n-мерная группа когомологий Чеха пространства Xсо значениями в
), не зависящий от вписывания т. n-мерная группа когомологий Чеха пространства Xсо значениями в  определяется формулой:
определяется формулой: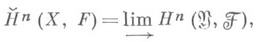
где индуктивный предел берется по направленному (по отношению вписанности) множеству классов открытых покрытий (два покрытия эквивалентны тогда и только тогда, когда каждое из них можно вписать в другое). Определение когомологий Чеха применимо и к предпучкам.
Недостатком когомологий Чеха является то, что они (для непаракомпактных пространств) не образуют когомологич. функтора (см. Гомологический функтор). В случае, когда
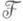 - постоянный пучок, соответствующий абелевой группе
- постоянный пучок, соответствующий абелевой группе  группы
группы  совпадают с когомологиями Александрова - Чеха с коэффициентами в группе
совпадают с когомологиями Александрова - Чеха с коэффициентами в группе 
Когомологии Гротеидика. Рассматривается функтор
 из категории пучков абелевых групп на Xв категорию абелевых групп. Правые производные этого функтора наз. n-мерными группами когомологий Гротендика со значениями впучке
из категории пучков абелевых групп на Xв категорию абелевых групп. Правые производные этого функтора наз. n-мерными группами когомологий Гротендика со значениями впучке  и обозначаются
и обозначаются 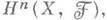 n=0, 1,... . Точной последовательности пучков абелевых групп
n=0, 1,... . Точной последовательности пучков абелевых групп
соответствует точная последовательность

т. е.
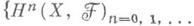 образуют когомологич. функтор. При этом
образуют когомологич. функтор. При этом 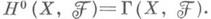 Если-
Если- 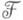 вя лый пучок, то
вя лый пучок, то  Эти три свойства когомологий Гротендика характеризуют функтор
Эти три свойства когомологий Гротендика характеризуют функтор 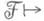
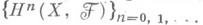 однозначно с точностью до изоморфизма.
однозначно с точностью до изоморфизма.Для вычисления когомологий Гротендика пучка
 можно воспользоваться левой резольвентой пучка
можно воспользоваться левой резольвентой пучка  состоящей из пучков, когомологий Гротендика к-рых равны 0 в положительных размерностях. Напр., на произвольных топологич. пространствах можно взять резольвенту из вялых пучков, а на паракомпактных пространствах - из мягкий пучков или из тонких пучков.
состоящей из пучков, когомологий Гротендика к-рых равны 0 в положительных размерностях. Напр., на произвольных топологич. пространствах можно взять резольвенту из вялых пучков, а на паракомпактных пространствах - из мягкий пучков или из тонких пучков.Когомологий Гротендика связаны с когомологиями покрытий следующим образом. Пусть
 -открытое покрытие пространства X. Тогда существует спектральная последовательность
-открытое покрытие пространства X. Тогда существует спектральная последовательность  сходящаяся к
сходящаяся к  и такая, что
и такая, что  где
где  - предпучок, сопоставляющий открытому множеству
- предпучок, сопоставляющий открытому множеству 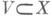 группу
группу  Если когомологий всех
Если когомологий всех  со значениями в
со значениями в  равны 0 в положительных размерностях, то последовательность вырождается и
равны 0 в положительных размерностях, то последовательность вырождается и 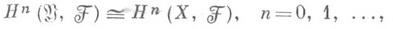 (теорема Лере). В общем случае спектральная последовательность определяет функторный гомоморфизм
(теорема Лере). В общем случае спектральная последовательность определяет функторный гомоморфизм  и, после перехода к пределу,- функторный гомоморфизм
и, после перехода к пределу,- функторный гомоморфизм 
Последний гомоморфизм биективен для n=0, 1, инъективен (но, вообще говоря, не сюръективен) для n=2 и биективен для всех п, если Xпаракомпактно. Таким образом, для паракомпактного пространства X
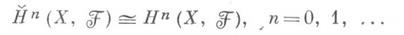
Обобщением определенных выше групп когомологий являются группы когомологий
 с носителями в семействе Ф. Семейство Ф замкнутых подмножеств пространства Xназ. семейством носителей, если 1) замкнутое подмножество любого множества из Ф принадлежит Ф; 2) объединение любых двух подмножеств из Ф лежит в Ф. Группы
с носителями в семействе Ф. Семейство Ф замкнутых подмножеств пространства Xназ. семейством носителей, если 1) замкнутое подмножество любого множества из Ф принадлежит Ф; 2) объединение любых двух подмножеств из Ф лежит в Ф. Группы  определяются как правые производные функтора
определяются как правые производные функтора 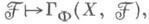 где Г Ф (Х,
где Г Ф (Х,  - группа сечений пучка
- группа сечений пучка 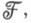 носители к-рых лежат в Ф. Они образуют когомологич. функтор.
носители к-рых лежат в Ф. Они образуют когомологич. функтор.Если Ф - семейство всех замкнутых множеств, то
 Другой важный частный случай: Ф = с - семейство всех компактных подмножеств. Группы
Другой важный частный случай: Ф = с - семейство всех компактных подмножеств. Группы 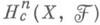 наз. группами когомоло-
наз. группами когомоло-гий с компактными носителями. В случае, когда F- пучок колец, в группе
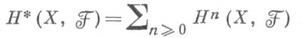
естественным образом определяется умножение, превращающее ее в градуированное кольцо (кольцо когомологий). При этом ассоциативность в пучке
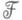 влечет за собой ассоциативность умножения в Н*(X,
влечет за собой ассоциативность умножения в Н*(X, а пучок коммутативных колец или колец Ли приводит к градуированно-коммутативному кольцу или градуированному кольцу Ли когомологий соответственно. Если
а пучок коммутативных колец или колец Ли приводит к градуированно-коммутативному кольцу или градуированному кольцу Ли когомологий соответственно. Если 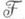 - пучок модулей над пучком колец
- пучок модулей над пучком колец  то
то 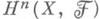 являются модулями над кольцом О
являются модулями над кольцом О  когомологиях со значениями в пучке неабелевых групп см. Неабелевы когомологий.
когомологиях со значениями в пучке неабелевых групп см. Неабелевы когомологий.Лит.:[1] Гротендик А., О некоторых вопросах гомологической алгебры, пер. с франц., М., 1961; [2] Годеман Р., Алгебраическая топология и теория пучков, пер. с франц., М., 1961; [3] Серр Ж.-П., в сб.: Расслоенные пространства, М., 1958, с. 372-450.
Д. А. Пономарев.
Когомологий пространства с операторами - когомологические инварианты топологич. пространства с заданным на нем действием группы. Пусть группа G действует на пространстве X, причем для каждого
 отображение
отображение  является гомеоморфизмом
является гомеоморфизмом  тогда G-пучком абелевых групп на X наз. пучок абелевых групп на Xвместе с заданным на нем действием группы G, к-рое непрерывно, согласовано с действием на Xи изоморфно отображает слои пучка друг на друга. В группе сечений G-пучка
тогда G-пучком абелевых групп на X наз. пучок абелевых групп на Xвместе с заданным на нем действием группы G, к-рое непрерывно, согласовано с действием на Xи изоморфно отображает слои пучка друг на друга. В группе сечений G-пучка  (и вообще в группах когомологий
(и вообще в группах когомологий  определена естественная структура G-модуля. G-пучки абелевых групп на Xобразуют абелову категорию, всякий объект к-рой вкладывается в инъективный объект. Функтор
определена естественная структура G-модуля. G-пучки абелевых групп на Xобразуют абелову категорию, всякий объект к-рой вкладывается в инъективный объект. Функтор 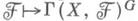 из этой категории в категорию абелевых групп, где
из этой категории в категорию абелевых групп, где 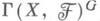 - группа G-инвариантных сечений G-пучка
- группа G-инвариантных сечений G-пучка  обладает правыми производными
обладает правыми производнымифункторами
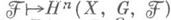 (n=0, 1, 2, ...), где
(n=0, 1, 2, ...), где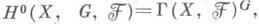 составляющими когомологич. функтор. Группы
составляющими когомологич. функтор. Группы 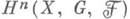 играют основную роль в изучении связи между когомологиями пространства X, факторпространства Y= X/G и группы G. Существует спектральная последовательность { Е r}со вторым членом
играют основную роль в изучении связи между когомологиями пространства X, факторпространства Y= X/G и группы G. Существует спектральная последовательность { Е r}со вторым членом 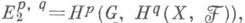 сходящаяся к
сходящаяся к  Пусть
Пусть 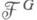 - пучок инвариантов прямого образа
- пучок инвариантов прямого образа 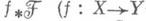 - естественная проекция), рассматриваемого как G-пучок на пространстве Y, на к-ром G действует тривиально. Если Gдействует на Xсобственно разрывно (см. Дискретная группа преобразований) и свободно, то
- естественная проекция), рассматриваемого как G-пучок на пространстве Y, на к-ром G действует тривиально. Если Gдействует на Xсобственно разрывно (см. Дискретная группа преобразований) и свободно, то 
 (см. [1]). В частности, если А- некоторый G-модуль, то постоянный пучок
(см. [1]). В частности, если А- некоторый G-модуль, то постоянный пучок  на Xобладает естественной структурой G-пучка, а пучок
на Xобладает естественной структурой G-пучка, а пучок  на Yбудет локально постоянным. В этом случае спектральная последовательность {Е r} удовлетворяет условию
на Yбудет локально постоянным. В этом случае спектральная последовательность {Е r} удовлетворяет условию 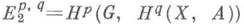 и сходится к
и сходится к 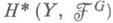 (спектральная последовательность накрытия). Если при этом Xсвязно и Н q( Х, А)=0 для q>0, то
(спектральная последовательность накрытия). Если при этом Xсвязно и Н q( Х, А)=0 для q>0, то  что дает топологич. интерпретацию когомологий группы G [2]. Если G собственно разрывна и Yпаракомпактно, то группы
что дает топологич. интерпретацию когомологий группы G [2]. Если G собственно разрывна и Yпаракомпактно, то группы  можно вычислять аналогично когомологиям Чеха при помощи G-инвариантных покрытий пространства X(см. [1]).
можно вычислять аналогично когомологиям Чеха при помощи G-инвариантных покрытий пространства X(см. [1]).В случае, когда G - группа Ли, дифференцируемо и свободно действующая на дифференцируемом многообразии X, причем X/G- дифференцируемое многообразие, известен аналог {Е r} спектральной последовательности накрытия [3]. Последовательность
 сходится к когомологиям комплекса G-инвариантных дифференциальных форм на X и
сходится к когомологиям комплекса G-инвариантных дифференциальных форм на X и  =
= где когомологии группы Gвычисляются при помощи коцепей класса
где когомологии группы Gвычисляются при помощи коцепей класса 
См. также Когомологии групп, Эквиеариаптные когомологии.
Лит.:[1]Гротендик А., О некоторых вопросах гомологической алгебры, пер. с франц., М., 1961; [2] Картан А., Эйленберг С., Гомологическая алгебра, пер. с англ., М., 1960; [3] van Est W. Т., "Proc. Nederl. Akad. Wetensch. Ser. A", 1958, v. 61, p. 399-413.
А. Л. Онищик, Д. А. Пономарев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
