- КВАТЕРНИОН
- гиперкомплексное число, геометрически реализуемое в четырехмерном пространстве. Система К. предложена в 1843 У. Гамильтоном (W. Hamilton). К. явились исторически первым примером гицеркомплексной системы, возникшей при попытках найти обобщение комплексных чисел. Комплексные числа изображаются геометрически точками плоскости, и действия над ними соответствуют простейшим геометрич. преобразованиям плоскости. Из точек пространства трех и выше измерений нельзя "устроить" числовую систему, подобную полю действительных или комплексных чисел. Однако, если отказаться от коммутативности умножения, то из точек 4-мерного пространства можно устроить числовую систему (в пространстве трех, пяти и выше измерений нельзя построить даже такую систему).
К. образуют 4-мерную алгебру над полем действительных чисел с базой 1, i, j, k("базисные единицы") и следующей таблицей умножения "базисных единиц":
1Х1 =1
1Х i = i
1 Хj = j
1 Хk = k
iХ1 = i
iХ i = -1
iХj = k
iХk =-j
jХ1 = j
j Хj=-k
jХj =-1
jХ k=i
kХ1 = k
kХ i=j
kХj = -i
k Хk= -1.
Всякий К. может быть записан в виде
или (поскольку 1 играет роль обычной единицы и в записи К. может быть опущена) в виде
Различаются скалярная часть К. х 0 и векторная часть
так что X=x0+V. Если х 0=0, то кватернион Vназ. вектором, и он может отождествляться с обычным 3-мерным вектором, поскольку умножение в алгебре К. двух таких векторов V1 и V2 связано со скалярным (V1, V2) и векторным [V1, V2]произведениями векторов Vx и V2 в 3-мерном пространстве формулой
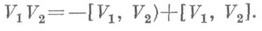
Это прказывает тесную связь К. с векторным исчислением. Исторически последнее и возникло из теории К. Всякому К. X=x0+V сопоставляется сопряженный кватернион Х=х 0-V, при этом
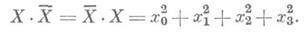
Это действительное число наз. нормой кватерниона Xи обозначается N(X). Норма К. удовлетворяет соотношению
Любое вращение 3-мерного пространства вокруг начала координат может быть задано при помощи кватерниона Рс нормой 1. Вращение, соответствующее Р, переводит вектор X = x1i+x2j+x3k в вектор Y=y1i+ у 2j+у 3k=РХР-1.
Алгебра К. является единственной ассоциативной, но не коммутативной, конечномерной нормированной алгеброй над полем действительных чисел, обладающей единицей. Алгебра К.- тело, т. е. в ней определено деление, причем К., обратным к К. X, является
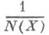X. Тело К. единственная конечномерная действительная ассоциативная, но не коммутативная алгебра без делителей нуля (см. также Фробениуса теорема).Лит.:[1] Калужнин Л. А., Введение в общую алгебру, М., 1973; [2] Кантор И. Л., Солодовников А. С, Гиперкомплексные числа, М., 1973; [3] Курош А. Г., Лекции по общей алгебре, 2 изд., М., 1973.
Н. Н. Вильямс.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
