Совершенное множество — замкнутое множество, не имеющее изолированных точек, то есть совпадающее с множеством всех своих предельных точек. Примеры Классическим примером нигде не плотного, совершенного множества является Канторово множество. Свойства Всякое непустое… … Википедия
Совершенное множество — замкнутое множество (См. Замкнутые множества), не имеющее изолированных точек, т. е. совпадающее с множеством всех своих предельных точек (См. Предельная точка). Классическим примером нигде не плотного; С. м. является Кантора множество.… … Большая советская энциклопедия
МНОЖЕСТВО ТИПА — множество ( множество), объединение (пересечение) счетного числа замкнутых (открытых) множеств. См. Борелевское множество. А МНОЖЕСТВО, аналитическое множество, в полном сепарабельном метрическом пространстве непрерывный образ борелевского… … Математическая энциклопедия
Совершенное число — (др. греч. ἀριθμὸς τέλειος) натуральное число, равное сумме всех своих собственных делителей (т. е. всех положительных делителей, отличных от самого числа). По мере того как натуральные числа возрастают, совершенные числа встречаются… … Википедия
Совершенное пространство — Совершенное топологическое пространство пространство, в котором каждое замкнутое множество является Gδ множеством, т.е. представимо в виде счётного пересечения открытых множеств.[1] Майкл в 1953 году доказал[2], что совершенные пространства… … Википедия
СОВЕРШЕННОЕ БИКОМПАКТНОЕ РАСШИРЕНИЕ — расширение Y вполне регулярного пространства X такое, что замыкание в Yграницы любого открытого множества служит границей O(U), где O(U) максимально открытое в У множество, для к рого Эквивалентные требования: а) для любой пары непересекающихся… … Математическая энциклопедия
Кантора множество — совершенное множество точек на прямой (см. Замкнутые множества), не содержащее ни одного отрезка; построено Г. Кантором (1883). Конструируется следующим образом (см. рис.): на отрезке [0, 1] удаляется интервал (1/3, 2/3), составляющий его … Большая советская энциклопедия
СОВЕРШЕННОЕ КОЛЬЦО — левое ассоциативное кольцо, каждый левый модуль над к рым обладает проективным накрытием. Правое совершенное кольцо определяется аналогично. Левое С. к. может и не быть правым С. к. Эквивалентны следующие свойства кольца R: (1) R левое С. к.; (2) … Математическая энциклопедия
СОВЕРШЕННОЕ ЧИСЛО — целое положительное число, обладающее свойством, что оно совпадает с суммой всех своих положительных делителей, отличных от самого этого числа. Таким образом, целое число является С. ч., если С. ч. являются, напр., числа 6, 28, 496, 8128,33550336 … Математическая энциклопедия
КАНТОРОВО МНОЖЕСТВО — подмножество отрезка [0, 1] числовой оси, состоящее из всех чисел вида где ei равно 0 или 2. Построено Г. Кантором (G. Cantor, 1883). Геометрич. его описание (см. рис.): из отрезка [0, 1] выбрасывается его средняя треть интервал , затем из… … Математическая энциклопедия
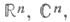 канторово множество.
канторово множество. 