ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ

ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ

для обыкновенного дифференциального уравнения 1-го порядка

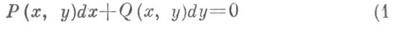
- функция 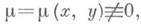обладающая тем свойством, что уравнение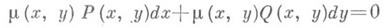

является дифференциальным уравнением в полных дифференциалах. Напр., для линейного уравнения y'+a(x)y=f(x), или (a(x)y-f(x))dx+dy=0, И. м. служит функция 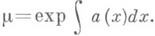Если уравнение (1) в области D, где 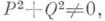имеет гладкий общий интеграл U(x, у) = С, то оно имеет бесконечно много И. м. Если функции Р( х, у), Q(x, у )имеют непрерывные частные производные в односвязной области D, где 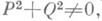то в качестве И. м. можно взять любое частное (нетривиальное) решение уравнения с частными производными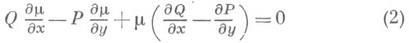

(см. [1]). Однако общего метода отыскания решений уравнения (2) не существует и поэтому фактическое нахождение И. м. для конкретного уравнения (1) удается лишь в исключительных случаях (см. [2]).

Лит.:[1] Степанов В. В., Курс дифференциальных уравнений, 9 изд., М., 1966; [2] Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976.

Н. X. Розов.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем решить контрольную работу

Смотреть что такое "ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ" в других словарях:

  • Интегрирующий множитель — Простейшие дифференциальные уравнения первого порядка  класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными …   Википедия

  • Интегрирующий множитель —         множитель, после умножения на который левая часть дифференциального уравнения (См. Дифференциальные уравнения)          P(x, y)dx + Q(x, y)dy = 0 (*)         обращается в полный дифференциал (см. Дифференциальное исчисление) некоторой… …   Большая советская энциклопедия

  • Простейшие дифференциальные уравнения первого порядка — Простейшие дифференциальные уравнения первого порядка  класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися… …   Википедия

  • АБСОЛЮТНАЯ ТЕМПЕРАТУРА — (термодинамическая температура), параметр состояния, характеризующий макроскопич. систему в состоянии термодинамич. равновесия (при этом А. т. всех её макроскопич. подсистем одинакова). А. т. введена в 1848 англ. физиком У. Томсоном (Кельвином)… …   Физическая энциклопедия

  • КЛАУЗИУСА НЕРАВЕНСТВО — выражает теорему термодинамики, согласно к рой для любого кругового процесса (цикла), совершённого системой, выполняется неравенство: где dQ кол во теплоты, поглощённой или отданной системой на бесконечно малом участке кругового процесса при темп …   Физическая энциклопедия

  • ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ — один из осн. законов термодинамики, устанавливающий необратимость реальных термодинамич. процессов. В. н. т. сформулировано как закон природы H. Л. С. Карно (N. L. S. Carnot) в 1824, P. Клаузиусом (R. Clausius) в 1850 и У. Томсоном (Кельвином) (W …   Физическая энциклопедия

  • ДАРБУ УРАВНЕНИЕ — 1) Д. у. обыкновенное дифференциальное уравнение где Р, Q, R целые многочлены относительно хи у. Это уравнение впервые исследовал Г. Дарбу [1]. Частный случай Д. у. Якоби уравнение. Пусть п высшая степень многочленов Р, Q, R;если Д. у. имеет s… …   Математическая энциклопедия

  • ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ — обыкновенное дифференциальное уравнение левая часть к рого может быть записана в виде полной производной: Другими словами, уравнение (1) является Д. у. в п. д., если существует такая дифференцируемая функция Ф( х, и 0, и 1, . .., и п 1), что… …   Математическая энциклопедия

  • Обыкновенное дифференциальное уравнение — Обыкновенные дифференциальные уравнения (ОДУ)  это дифференциальное уравнение вида где   неизвестная функция (возможно, вектор функция, тогда , как правило, тоже вектор функция со значениями в пространстве той же размерности; в этом… …   Википедия

  • Мю (буква) — Греческий алфавит Α α  альфа Β β  бета …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»