- ДЖЕКСОНА НЕРАВЕНСТВО
- неравенство, дающее оценку скорости убывания наилучшего приближения функции тригонометрия, полиномами или алгебраич. многочленами в зависимости от ее дифференциально-разностных свойств. Пусть f(x)- непрерывная на всей оси 2p-периодич. функция, En(f)- наилучшее равномерное приближение f(x)тригонометрия, полиномами Т п (х)порядка п, т. е.
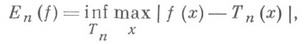
и

- модуль непрерывности функции f(x). Д. Джексон [1] показал, что
 (*)
(*)(С - абсолютная константа), а если f(x)имеет r- юнепрерывную производную f(r)(x),
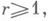 то
то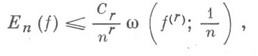
где постоянная С r зависит только от r. В случае
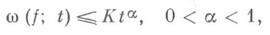
неравенство (*) было независимо получено С. Н. Бернштейном [3].
Если f(х)непрерывна или г раз непрерывно дифференцируема на отрезке [а, 6], г=1,2..., и En(f; а, b)- наилучшее равномерное приближение функции f(x)па [а, b]алгебраич. многочленами степени п, то для п>r имеет место соотношение (f0(x)=f(x))

где постоянная А r зависит только от r.
Д. н. известны также как теоремы Джексона, или прямые теоремы теории приближения функций. Они обобщались в различных направлениях: приближение в интегральной метрике, приближение целыми функциями конечной степени, оценка приближения через модуль гладкости k-го порядка, функции многих переменных. В ряде случаев в Д. н. найдены точные значения констант.
Лит.:[1] Jackson D., t)ber die Genauigkeit dor Annaherung stetiger Punktionen durch ganze rationale Punktionen, Dissertation, Gott., 1911; [2] Никольский С. М., Приближение функций многих переменных и теоремы вложения, М., 1969; [3] Бернштсйн С. Н., "Сооб. Харьк. матем. общества", сер. 2, 1912, т. 13, с. 49-194; [4] Корнейчук Н. П., Экстремальные задачи теории приближения, М., 1976.
Н. П. Корнейчук, В. П. Моторный.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
