АЛГЕБРАИЧЕСКАЯ ТОЧКА ВЕТВЛЕНИЯ
- АЛГЕБРАИЧЕСКАЯ ТОЧКА ВЕТВЛЕНИЯ
а л-гебраическая особая точка,- изолированная точка ветвления аконечного порядка аналитич. функции  обладающая тем свойством, что для любого элемента аналитич. родолжения этой функции, регулярного в области, имеющей точку а граничной точкой, существует предел
обладающая тем свойством, что для любого элемента аналитич. родолжения этой функции, регулярного в области, имеющей точку а граничной точкой, существует предел  Точнее, точка а плоскости комплексного переменного
Точнее, точка а плоскости комплексного переменного  , являющаяся особой для полной аналитической функции
, являющаяся особой для полной аналитической функции при продолжении нек-рого правильного элемента
при продолжении нек-рого правильного элемента  этой функции с центром
этой функции с центром  вдоль путей, проходящих через а, наз. алгебраической точкой ветвления, если выполняются следующие условия. 1) Существует такое положительное число
вдоль путей, проходящих через а, наз. алгебраической точкой ветвления, если выполняются следующие условия. 1) Существует такое положительное число  , что элемент
, что элемент  может быть продолжен вдоль любой непрерывной кривой, лежащей в кольце
может быть продолжен вдоль любой непрерывной кривой, лежащей в кольце  2) Существует такое натуральное
2) Существует такое натуральное  , что если
, что если  - любая точка кольца D, то аналитич. родолжение элемента
- любая точка кольца D, то аналитич. родолжение элемента 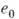 в кольце Dдает в точности kразличных элементов функции
в кольце Dдает в точности kразличных элементов функции  с центром
с центром  ; если
; если  -какой-либо элемент с центром
-какой-либо элемент с центром  , то все остальные
, то все остальные  элементов с центром
элементов с центром  получаются аналитич. родолжением по замкнутым путям, охватывающим точку а. 3) Значения всех элементов, получаемых из
получаются аналитич. родолжением по замкнутым путям, охватывающим точку а. 3) Значения всех элементов, получаемых из  продолжением в Dв точках
продолжением в Dв точках  кольца D, стремятся к определенному, конечному пли бесконечному, пределу, когда
кольца D, стремятся к определенному, конечному пли бесконечному, пределу, когда  стремится к а, оставаясь в D.
стремится к а, оставаясь в D.
Число k-1 наз. порядком А. т. в. Все ветви функции  получаемые аналитнч. продолжением элемента
получаемые аналитнч. продолжением элемента  в кольце D, могут быть представлены в проколотой окрестности точки апри помощи обобщенного ряда Лорана (ряда Пюизё):
в кольце D, могут быть представлены в проколотой окрестности точки апри помощи обобщенного ряда Лорана (ряда Пюизё):

Бесконечно удаленная точка  наз. А. т. в. для функции
наз. А. т. в. для функции , если точка
, если точка  является А. т. в. функции
является А. т. в. функции 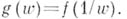
Может существовать несколько (и даже бесконечно много) различных А. т. в. и правильных точек полной аналитпч. функции с одним и тем же аффиксом а.
Лит.:[1] Маркушевич А. И., Теория аналитических Функций, 2 изд., т. 2, М., 1968, гл. 8; [2] Гурвиц А., Курант Р., Теория функций, пер. с нем., М., 1968, ч. 3, гл. 4.
Е. Д. Соломснцев.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "АЛГЕБРАИЧЕСКАЯ ТОЧКА ВЕТВЛЕНИЯ" в других словарях:
ВЕТВЛЕНИЯ ТОЧКА — особая точка многозначного характера, изолированная особая точка а аналитич. функции одного комплексного переменного такая, что аналитическое продолжение к. л. элемента функции вдоль замкнутого пути, охватывающего а, приводит к новым элементам .… … Математическая энциклопедия
ПОДВИЖНАЯ ОСОБАЯ ТОЧКА — особая точка z0 решения дифференциального уравнения F(z, w, w )=0 (F аналитич. функция), рассматриваемого как функция w(z).комплексного переменного z, при условии, что решения того же уравнения с близкими начальными данными имеют близкие к z0… … Математическая энциклопедия
АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ — функция переменных x1,...xn удовлетворяющая уравнению где F неприводимый многочлен от с коэффициентами из нек рого поля K, наз. полем констант. А. ф., заданная над этим полем, наз. А. ф. над полем K. Многочлен часто записывается по степеням… … Математическая энциклопедия
Ряд Пюизё — (дробно степенной ряд) обобщение понятия степенного ряда, в котором используются не только целые, но и дробные (рациональные) показатели; допускаются также отрицательные показатели. Ряды Пюизё находят применение в различных разделах математики, в … Википедия
ДВОЙНАЯ ПЛОСКОСТЬ — алгебраическая поверхность, представляющая собой двумерный аналог гиперэллиптической кривой. Неособая алгебраическая проективная поверхность Xнад алгебраически замкнутым полем кназ. двойной плоскостью, если ее поле рациональных функций… … Математическая энциклопедия
Калькулятор — У этого термина существуют и другие значения, см. Калькулятор (значения). Современный инженерный калькулятор Калькулятор … Википедия
Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия
АНАЛИТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ — раздел теории обыкновенных дифференциальных уравнений, в к ром решения исследуются с точки зрения теории аналитич. функций. Типичная постановка задачи в А. т. д. у. такова: дан нек рый класс дифференциальных уравнений, все решения к рых суть… … Математическая энциклопедия
ПОЛЕЙ КЛАССОВ ТЕОРИЯ — теория, дающая описание всех абелевых расширений (конечных расширений Галуа с абелевой группой Галуа) поля К, принадлежащего к одному из следующих типов: 1) К поле алгебраич. чисел, т. е. конечное расширение поля ; 2) К конечное расширение поля… … Математическая энциклопедия
Трансцендентные функции — аналитические функции, не являющиеся алгебраическими (см. Алгебраические функции (См. Алгебраическая функция)). Простейшими примерами Т. ф. служат Показательная функция, Тригонометрические функции, Логарифмическая функция. Если Т. ф.… … Большая советская энциклопедия
 обладающая тем свойством, что для любого элемента аналитич. родолжения этой функции, регулярного в области, имеющей точку а граничной точкой, существует предел
обладающая тем свойством, что для любого элемента аналитич. родолжения этой функции, регулярного в области, имеющей точку а граничной точкой, существует предел  Точнее, точка а плоскости комплексного переменного
Точнее, точка а плоскости комплексного переменного  , являющаяся особой для полной аналитической функции
, являющаяся особой для полной аналитической функции при продолжении нек-рого правильного элемента
при продолжении нек-рого правильного элемента  этой функции с центром
этой функции с центром  вдоль путей, проходящих через а, наз. алгебраической точкой ветвления, если выполняются следующие условия. 1) Существует такое положительное число
вдоль путей, проходящих через а, наз. алгебраической точкой ветвления, если выполняются следующие условия. 1) Существует такое положительное число  , что элемент
, что элемент  может быть продолжен вдоль любой непрерывной кривой, лежащей в кольце
может быть продолжен вдоль любой непрерывной кривой, лежащей в кольце  2) Существует такое натуральное
2) Существует такое натуральное  , что если
, что если  - любая точка кольца D, то аналитич. родолжение элемента
- любая точка кольца D, то аналитич. родолжение элемента 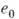 в кольце Dдает в точности kразличных элементов функции
в кольце Dдает в точности kразличных элементов функции  с центром
с центром  ; если
; если  -какой-либо элемент с центром
-какой-либо элемент с центром  , то все остальные
, то все остальные  элементов с центром
элементов с центром  получаются аналитич. родолжением по замкнутым путям, охватывающим точку а. 3) Значения всех элементов, получаемых из
получаются аналитич. родолжением по замкнутым путям, охватывающим точку а. 3) Значения всех элементов, получаемых из  продолжением в Dв точках
продолжением в Dв точках  кольца D, стремятся к определенному, конечному пли бесконечному, пределу, когда
кольца D, стремятся к определенному, конечному пли бесконечному, пределу, когда  стремится к а, оставаясь в D.
стремится к а, оставаясь в D. получаемые аналитнч. продолжением элемента
получаемые аналитнч. продолжением элемента  в кольце D, могут быть представлены в проколотой окрестности точки апри помощи обобщенного ряда Лорана (ряда Пюизё):
в кольце D, могут быть представлены в проколотой окрестности точки апри помощи обобщенного ряда Лорана (ряда Пюизё):
 наз. А. т. в. для функции
наз. А. т. в. для функции , если точка
, если точка  является А. т. в. функции
является А. т. в. функции