ВЕТВЛЕНИЯ ТОЧКА

особая точка многозначного характера,- изолированная особая точка а аналитич. функции одного комплексного переменного такая, что аналитическое продолжение к.-л. элемента функции 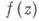вдоль замкнутого пути, охватывающего а, приводит к новым элементам 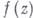. Точнее, аназ. В. т., если существуют: 11 кольцо 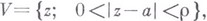в к-ром аналитически продолжается по любому пути; 2) точка и к.-л. элемент функции , представленный степенным рядом

с центром и радиусом сходимости аналитич. родолжение к-рого вдоль окружности 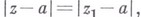проходимой один раз, напр, в положительном направлении, приводит к новому элементу 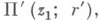отличающемуся от Если после нек-рого минимального числа таких обходов снова получается исходный элемент то это же самое будет иметь место для всех элементов ветви аналитической функции , определяемой в V элементом В таком случае аявляется В. т. конечного порядка для указанной ветви. В проколотой окрестности VВ. т. аконечного порядка эта ветвь представима в виде обобщенного ряда Лорана, или ряда Пюизё:

Если - бесконечно удаленная В. т. конечного порядка, то в нек-рой окрестности данная ветвь 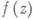представима в виде аналога ряда (1):

Поведение римановой поверхности R функции 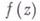над В. т. конечного порядка а характеризуется тем, что над асоединяются вместе kлистов той ветви , к-рая определяется элементом При этом поведение других ветвей Rнад аможет быть совершенно иным.

Если в ряде (1) или (2) среди коэффициентов 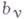с отрицательными индексами v имеется лишь конечное число отличных от нуля, то а - алгебраическая точка ветвления, или алгебраическая особая точка. Такая В. т. конечного порядка характеризуется также тем, что при любом стремлении в или 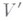значения всех элементов ветви, определяемой стремятся к определенному конечному или бесконечному пределу.

Пример: 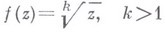-натуральное число,

Если в ряде (1) или (2) имеется бесконечно много ненулевых коэффициентов b_V с отрицательными индексами v, то В. т. конечного порядка аотносится к классу трансцендентных В. т. Пример: 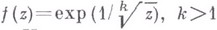- натуральное число,.

Наконец, если ни при каком числе последовательных обходов нельзя возвратиться к исходному элементу, то аназ. логарифмической точкой ветвления, или В. т. бесконечного порядка, и также относится к трансцендентным В. т. Пример: 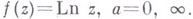Над логарифмич. В. т. соединяются бесконечно много листов той ветви , к-рая определяется элементом

В случае аналнтич. функции многих комплексных переменных точка апространства или наз. В. т. порядка т, если она является В. т. порядка т, вообще говоря, мно-голистной голоморфности области функции 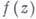. В отличие от случая , при В. т., как и другие особые точки аналитических функций многих комплексных переменных, не могут быть изолированными.

Лит.:[1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968, гл. 8; [2] Фукс Б. А., Теория аналитических функций многих комплексных переменных, 2 изд., М., 1962, ч. 1, гл. 2. Е. Д. Соломтцев.