ГЛАВНЫХ ИДЕАЛОВ КОЛЬЦО

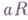ассоциативное кольцо R с единицей, в к-ром все левые п правые идеалы являются главными, т. е. имеют вид и , соответственно, где . Примеры Г. и. к.: кольцо целых чисел, кольцо многочленов над полем F, кольцо косых многочленов над полем Fс автоморфизмом (элементы имеют вид сложение этих элементов обычное, а определяется умножение законами дистрибутивности и равенством , где ), кольцо дифференциальных многочленов над полем Fс дифференцированием (это кольцо также состоит из элементов причем сложение обычное, а умножение определяется равенством , где ). Г. и. к. без делителей нуля наз. областью главных идеалов. Коммутативное Г. п. к. является прямой суммой областей главных идеалов п Г. и. к., обладающих единственным простым идеалом, к-рый нильпотентен (см. [2], с. 282). Если R - область главных идеалов, то два ненулевые элемента а, b кольца R имеют наибольший общий левый делитель ( а, b).и наименьшее общее правое кратное , к-рые определяются как элементы, удовлетворяющие равенствам:

Элементы единственны с точностью до обратимого правого множителя. Область главных идеалов является областью с однозначным разложением на множители. Двусторонние идеалы области главных идеалов образуют относительно умножения свободную коммутативную полугруппу с нулем и единицей (свободными порождающими этой полугруппы будут максимальные идеалы кольца).

Подмодуль Nсвободного модуля Мконечного ранга пнад Rявляется свободным модулем ранга над R, п в модулях Ми Nможно так выбрать базисы и что где и является полным (т. е. ) делителем элементов при . Каждый конечно порожденный модуль Кнад Rявляется прямой суммой циклич. модулей , , где и - полный делитель при . Эта теорема обобщает основную теорему о конечно порожденных абелевых группах. Элементы из предыдущей теоремы определены однозначно с точностью до подобия (см. Ассоциативные кольца и алгебры). Эти элементы наз. инвариантными множителями модуля К. Кроме того, модуль K можно представить в виде прямой суммы далее неразложимых цнклич. модулей где Элементы определены однозначно С точностью до подобия и наз. элементарными делителями модуля К. Если область Rглавных идеалов коммутативна, то или где 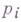- неприводимые (простые) элементы кольца R. Из предыдущих утверждений вытекают обычные свойства элементарных делителей и инвариантных множителей линейных преобразований конечномерных векторных пространств [3].

Лит.:[1] Джекобсон Н., Теория колец, пер. с англ., М., 1947; [2] Зарисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1963; [3] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. о франц., М., 1966. Л. А. Бакуть.