ГИББСА РАСПРЕДЕЛЕНИЕ

распределение вероятностей обнаружения равновесной статистич. системы в любом из ее стационарных микроскопич. состояний. Последние обычно задаются как чистые квантово-механич. состояния, определяемые решением y_n стационарного Шрёдингера уравнения

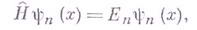
где п - полный набор квантовых чисел, фиксирующих каждое из этих состояний. Сопоставление каждому состоянию пвероятности обнаружения системы в этом состоянии (для непрерывного спектра величин n - плотности вероятности) полностью определяет, вместе с набором функций , так наз. смешанное кван-товомеханич. состояние. Для такого состояния наблюдаемые величины определяются как средние по распределению от квантовомеханич. средних для каждого чистого состояния п. Смешанное состояние полностью характеризуется статистич. оператором Неймана (матрицей плотности), к-рый в х - представлении имеет вид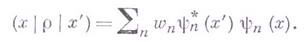

Наблюдаемые средние определяются как

В случае Г. р. смешанное состояние соответствует равновесному термодинамич. состоянию системы. Так как Г. р. имеют структуру где А - совокупность термодинамич. параметров, фиксирующих микроскопич. состояние системы, то соответствующие им операторы 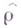выражаются непосредственно через оператор Гамильтона, В зависимости от выбора параметров A возможны различные формы Г. р., из к-рых наиболее распространены следующие.

Микроканоническое Г. р. Параметры Ахарактеризуют состояние изолированной системы и включают энергию , объем V, внешние поля аи число частиц 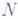(в случае многокомпонентной системы - совокупность чисел ). В этом случае Г. р. имеет вид

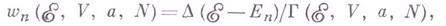
где Г- статистический вес, определяющий нормировку распределения и равный

причем сумма (или интеграл) берется по всем различным состояниям системы вне зависимости от их вырожденности по . Функция равна единице, если значение попадает в энергетич. слой около значения , и нулю в противном случае. Ширина должна быть значительно меньше макроскопических бесконечно малых изменений энергии , но не меньше интервала между уровнями энергии 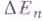. Статнстич. вес Г определяет число мнкроскопич. способов, к-рыми может осуществляться данное макроскопич. состояние и к-рые предполагаются равновероятными; он связан с энтропией системы выражением

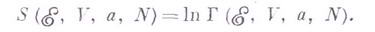
Каноническое Г. р. Макроканонич. состояние системы фиксируется температурой и величинами V, а. N (система "в термостате"); с точки зрения приложений это наиболее удобный способ задания термодинамич. состояния. Канонич. Г. р. имеет вид

где Z - статистическая сумма (или сумма состояний)

непосредственно связана со свободной энергией системы выражением

Большое каноническое Г. р. Параметры Афиксируют состояние системы в термостате, ограниченном воображаемыми стенками, свободно пропускающими частицы. Это 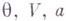и химич. потенциал m (в случае многокомпонентной системы - несколько химич. потенциалов). Г. р. по микроскопич. состояниям, определяемым числом частиц Nи квантовыми числами 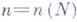системы Nтел, имеет вид

где - большая сумма состояний

определяющая нормировку этого распределения, связана с термодинамич. потенциалом ( р - давление) соотношением

Использование какого-либо Г. р. позволяет на основе микроскопич. задания статистич. системы рассчитать характерные для нее макроскопич. средние, дисперсии и т. д., а при помощи нормировочных сумм или 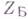- определить все термодинамич. характеристики равновесной системы. Выбор того пли иного Г. р. производится из соображений удобства. В статистическом предельном случае получаемые при помощи Г. р. результаты (выраженные в одних н тех же переменных) в главных асимптотиках по N одинаковы. А так как метод Гиббса гарантирует только такие асимптотики, то все варианты Г. р. оказываются идентичными. Микроканонич. Г. р. используется в основном применительно к общим вопросам статистич. механики (параметры Ане включают специфичных термодинамич. величин типа н т. и.), канонич. Г. р.- главным образом при рассмотрении классич. систем, большое канонич. Г. р.- при исследованиях квантовых систем, когда фиксация точного числа N по технич. соображениям неудобна.

При определенных значениях параметров А, связываемых обычно с повышением (при фиксированных остальных параметрах) сверх определенной температуры вырождения (имеющей разные значения для каждого вида микроскопич. движения), общие Г. р. переходят в квазиклассические (по отношению к переменным, для к-рых связанное с их изменением движение невырождено). В случае невырожденной системы N частиц, когда микроскопич. движение представляется как классич. движение N материальных точек, микроскопич. состояние задается фазовой точкой энергия определяется классич. гамильтонианом 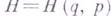, а канонич. Г. р. имеет вид

где классич. интеграл состояний (квазиклассич. предел статистич. суммы) равен

Г. р. введены Дж. Гиббсом (J. Gibbs, 1902).

Лит.: [1] Гиббс Д ж. В., Основные принципы статистической механики..., пер. с англ., М., 1946; [2] Xуанг К., Статистическая механика, пер. с англ.. М., 1966; [3] Леонтович М. А., Статистическая физика, М.- Л., 1944.

И. А. Квасников.