ГИББСА БОЛЬШОЕ КАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
- ГИББСА БОЛЬШОЕ КАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
- ГИББСА БОЛЬШОЕ КАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
-
распределение вероятностей состояний статистического ансамбля систем, к-рые находятся в тепловом и материальном равновесии со средой (термостатом и резервуаром ч-ц) и могут обмениваться с ними энергией и ч-цами (через полупроницаемые перегородки) при пост. объёме. Г. б. к. р.— статистич. распределение, соответствующее Гиббса большому каноническому ансамблю. Установлено амер. физиком Дж. У. Гиббсом (J. W. Gibbs) в 1901 как фундам. закон статистической физики. В классич. статистике вероятность распределения по состояниям определяется ф-цией распределения f(p, q), зависящей от координат q и импульсов р всех ч-ц системы. Вероятность пребывания N частиц в бесконечно малом фазовом объёме dpdq равна
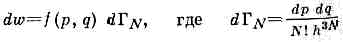 .
. Полная вероятность пребывания системы в к.-л. из состояний равна единице (она достоверно находится в одном из состояний), откуда следует, что
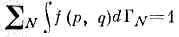 .
. (условие нормировки).
Равновесная ф-ция распределения, согласно Г. б. к. р., зависит от координат и импульсов через Гамильтона функцию HN(p,q) системы
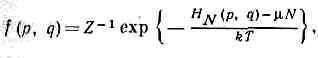 .
. 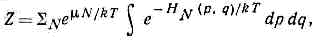 .
. где суммирование ведётся по всем целым положит. N, а интегрирование — по фазовому пр-ву N ч-ц. Т. о., Z выражается через статистич. интегралы для N ч-ц и зависит от m, V, Т.
Г. б. к. р. можно вывести из микроканонического распределения Гиббса, если рассматривать данную систему вместе с термостатом и резервуаром ч-ц как одну большую замкнутую и изолиров. систему и применить к ней микроканонич. распределение. Тогда малая подсистема обладает Г. б. к. р., к-рое можно найти интегрированием по фазовым переменным термостата и резервуара ч-ц и суммированием по числам ч-ц (теорема Гиббса).
В квант. статистике статистич. ансамбль характеризуется распределением
вероятности wi,N, квант. состояний г с энергией ?i,N, соответствующих числу ч-ц N, с условием нормировки Si,N WI,N= l. Г. б. к. р. для квант. систем имеет вид:
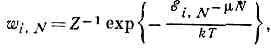 .
. где Z —
статистическая сумма для большого канонич. ансамбля Гиббса, определяемая из условия нормировки и равная:
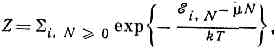 .
. Г. б. к. р. в квант. случае можно представить через матрицу плотности r=Z-1ехр{(H-mN)/kT}, где H —
гамильтониан системы.
Г. б. к. р. как в классич., так и в квант. случае позволяет вычислить
потенциал термодинамический F в переменных m, V, Т, равный: F=-kTlnZ. Г. б. к. р. не требует выполнения дополнит. условия, связанного с постоянством числа ч-ц, и поэтому удобно для практич. вычислений.
Физический энциклопедический словарь. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1983.
.
Полезное
Смотреть что такое "ГИББСА БОЛЬШОЕ КАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ" в других словарях:
большое каноническое распределение Гиббса — didysis kanoninis Gibso skirstinys statusas T sritis fizika atitikmenys: angl. grand canonical distribution vok. große kanonische Verteilung, f rus. большое каноническое распределение Гиббса, n pranc. distribution grande canonique, f; grande… … Fizikos terminų žodynas
МИКРОКАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ГИББСА — равновесное распределение вероятностей состояний статистического ансамбля систем с заданной полной энергией при пост. объёме и пост. числе ч ц, но энергетически изолированных от окружающей среды, т. е. статистич. распределение для… … Физическая энциклопедия
ГИББСА РАСПРЕДЕЛЕНИЕ — распределение вероятностей обнаружения равновесной статистич. системы в любом из ее стационарных микроскопич. состояний. Последние обычно задаются как чистые квантово механич. состояния, определяемые решением yn стационарного Шрёдингера уравнения … Математическая энциклопедия
ЭНТРОПИЯ — (от греч. entropia поворот, превращение), понятие, впервые введённое в термодинамике для определения меры необратимого рассеяния энергии. Э. широко применяется и в др. областях науки: в статистической физике как мера вероятности осуществления к.… … Физическая энциклопедия
Микроканонический ансамбль — Статистический ансамбль для изолированных (не обменивающихся энергией с окружающими телами) макроскопических систем в постоянном объёме при постоянном числе частиц; энергия систем М. а. имеет строго постоянное значение. Понятие М. а.,… … Большая советская энциклопедия
Флуктуации — (от лат. fluctuatio – колебание) случайные отклонения наблюдаемых физических величин от их средних значений. Ф. происходят у любых величин, зависящих от случайных факторов и описываемых методами статистики (см. Случайный процесс).… … Большая советская энциклопедия
Энтропия — (от греч. entropía поворот, превращение) понятие, впервые введенное в термодинамике (См. Термодинамика) для определения меры необратимого рассеяния энергии. Э. широко применяется и в других областях науки: в статистической физике (См.… … Большая советская энциклопедия
didysis kanoninis Gibso skirstinys — statusas T sritis fizika atitikmenys: angl. grand canonical distribution vok. große kanonische Verteilung, f rus. большое каноническое распределение Гиббса, n pranc. distribution grande canonique, f; grande distribution canonique, f … Fizikos terminų žodynas
distribution grande canonique — didysis kanoninis Gibso skirstinys statusas T sritis fizika atitikmenys: angl. grand canonical distribution vok. große kanonische Verteilung, f rus. большое каноническое распределение Гиббса, n pranc. distribution grande canonique, f; grande… … Fizikos terminų žodynas
grand canonical distribution — didysis kanoninis Gibso skirstinys statusas T sritis fizika atitikmenys: angl. grand canonical distribution vok. große kanonische Verteilung, f rus. большое каноническое распределение Гиббса, n pranc. distribution grande canonique, f; grande… … Fizikos terminų žodynas
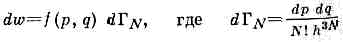 . элемент фазового объёма системы в ед. h3N, a N! учитывает, что перестановка тождеств. ч-ц не меняет состояния (см. ТОЖДЕСТВЕННОСТИ ПРИНЦИП).Полная вероятность пребывания системы в к.-л. из состояний равна единице (она достоверно находится в одном из состояний), откуда следует, что
. элемент фазового объёма системы в ед. h3N, a N! учитывает, что перестановка тождеств. ч-ц не меняет состояния (см. ТОЖДЕСТВЕННОСТИ ПРИНЦИП).Полная вероятность пребывания системы в к.-л. из состояний равна единице (она достоверно находится в одном из состояний), откуда следует, что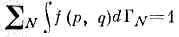 . (условие нормировки).Равновесная ф-ция распределения, согласно Г. б. к. р., зависит от координат и импульсов через Гамильтона функцию HN(p,q) системы
. (условие нормировки).Равновесная ф-ция распределения, согласно Г. б. к. р., зависит от координат и импульсов через Гамильтона функцию HN(p,q) системы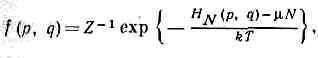 . где m — химический потенциал, Z — постоянная, определяемая из условия нормировки и равная:
. где m — химический потенциал, Z — постоянная, определяемая из условия нормировки и равная: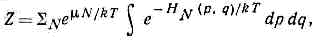 . где суммирование ведётся по всем целым положит. N, а интегрирование — по фазовому пр-ву N ч-ц. Т. о., Z выражается через статистич. интегралы для N ч-ц и зависит от m, V, Т.Г. б. к. р. можно вывести из микроканонического распределения Гиббса, если рассматривать данную систему вместе с термостатом и резервуаром ч-ц как одну большую замкнутую и изолиров. систему и применить к ней микроканонич. распределение. Тогда малая подсистема обладает Г. б. к. р., к-рое можно найти интегрированием по фазовым переменным термостата и резервуара ч-ц и суммированием по числам ч-ц (теорема Гиббса).В квант. статистике статистич. ансамбль характеризуется распределением вероятности wi,N, квант. состояний г с энергией ?i,N, соответствующих числу ч-ц N, с условием нормировки Si,N WI,N= l. Г. б. к. р. для квант. систем имеет вид:
. где суммирование ведётся по всем целым положит. N, а интегрирование — по фазовому пр-ву N ч-ц. Т. о., Z выражается через статистич. интегралы для N ч-ц и зависит от m, V, Т.Г. б. к. р. можно вывести из микроканонического распределения Гиббса, если рассматривать данную систему вместе с термостатом и резервуаром ч-ц как одну большую замкнутую и изолиров. систему и применить к ней микроканонич. распределение. Тогда малая подсистема обладает Г. б. к. р., к-рое можно найти интегрированием по фазовым переменным термостата и резервуара ч-ц и суммированием по числам ч-ц (теорема Гиббса).В квант. статистике статистич. ансамбль характеризуется распределением вероятности wi,N, квант. состояний г с энергией ?i,N, соответствующих числу ч-ц N, с условием нормировки Si,N WI,N= l. Г. б. к. р. для квант. систем имеет вид: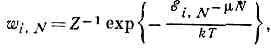 . где Z — статистическая сумма для большого канонич. ансамбля Гиббса, определяемая из условия нормировки и равная:
. где Z — статистическая сумма для большого канонич. ансамбля Гиббса, определяемая из условия нормировки и равная: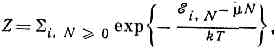 . Г. б. к. р. в квант. случае можно представить через матрицу плотности r=Z-1ехр{(H-mN)/kT}, где H — гамильтониан системы.Г. б. к. р. как в классич., так и в квант. случае позволяет вычислить потенциал термодинамический F в переменных m, V, Т, равный: F=-kTlnZ. Г. б. к. р. не требует выполнения дополнит. условия, связанного с постоянством числа ч-ц, и поэтому удобно для практич. вычислений.
. Г. б. к. р. в квант. случае можно представить через матрицу плотности r=Z-1ехр{(H-mN)/kT}, где H — гамильтониан системы.Г. б. к. р. как в классич., так и в квант. случае позволяет вычислить потенциал термодинамический F в переменных m, V, Т, равный: F=-kTlnZ. Г. б. к. р. не требует выполнения дополнит. условия, связанного с постоянством числа ч-ц, и поэтому удобно для практич. вычислений.