- РАСПРЕДЕЛЕНИЕ ГИПЕРГЕОМЕТРИЧЕСКОЕ
- — распределение вероятностей случайной величины т такой, что если из совокупности объема N извлекается случайная выборка без возвращения объема n, причем из всех элементов исходной совокупности определенным свойством обладало М элементов и М < N, то количество элементов с этим свойством в выборке из п элементов и будет случайной величиной т. Формула распределения вероятностей m:
, если max (0, M+n-N) ≤ I ≤ min (M,n); 0 — в остальных случаях.Математические ожидание:
}
(*)
Дисперсия
Если Dm>9, то Р. г. аппроксимируется нормальным распределением с параметрами (*):
.Если п и М не превышают 0,1N, то Р. г. близко к распределению Пуассона с параметром:
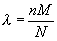. При N→∞, фиксированzных n и 
, причем n < 0,1N, P. г. сходится к биномиальному: Рп,M(т)→Сmnрт(1— р)n-т. При N ≥ 25, любых М и п возможна аппроксимация распределением β. Р. г. наблюдается во многих практических задачах, в частности, при выборке из общей совокупности правых и левых к-лов кварца.
Геологический словарь: в 2-х томах. — М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978.
