Теорема синусов (сферическая геометрия)

Сферическая теорема синусов устанавливает пропорциональность между синусами сторон a, b, c и синусами противолежащих этим сторонам углов A, B, C сферического треугольника:

$\frac{\sin a}{\sin A}=\frac{\sin b}{\sin B}=\frac{\sin c}{\sin C}.$

Сферическая теорема синусов является аналогом плоской теоремы синусов и переходит в последнюю в пределе малости сторон треугольников по сравнению с радиусом сферы.

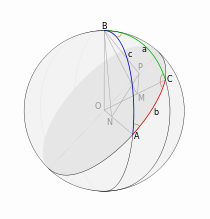
Доказательство  

Рисунок к доказательству теоремы синусов с помощью проекций.

Доказательство с помощью проекций^[1]. На рисунке показан сферический треугольник ABC на сфере радиуса R с центром в точке O. BP — перпендикуляр к плоскости большого круга, проходящего через сторону b, BM — перпендикуляр к OC, BN — перпендикуляр к OA. По утверждению, обратному теореме о трёх перпендикулярах, PM — перпендикуляр к OC, PN — перпендикуляр к OA. Заметим, что угол PMB равен π — C, кроме того, BN = R sin c и BM = R sin a. Далее, проецируем BN и BM на BP, получаем:

$BP = BN \sin \angle BNP = R \sin c \sin A,$

$BP = BM \sin \angle PMB = R \sin a \sin (\pi - C) = R \sin a \sin C,$

$\frac{\sin a}{\sin A}=\frac{\sin c}{\sin C}$

Аналогично получаем второе равенство.

Доказательство, опирающееся на уже доказанные соотношения между сторонами и углами сферического прямоугольного треугольника. Опустим из вершины C перпендикуляр CD = h на сторону с или её продолжение. Выразим h двояким образом из возникших при этом прямоугольных треугольников ACD и BCD:

$~\sin h=\sin b\sin A = sin a\sin B.$

Отсюда получаем пропорцию

$\frac{\sin a}{\sin A}=\frac{\sin b}{\sin B},$

к которой аналогичным образом добавляем отношение третьей пары «сторона-угол».

История

Теорема синусов для сферических треугольников была сформулирована и доказана в сочинениях ряда математиков средневекового Востока, живших в X веке н. э. — Абу-л-Вафы, ал-Ходжанди и Ибн Ирака. Эта теорема позволила упростить решения ряда задач сферической астрономии, которые до этого решались с помощью теоремы Менелая для полного четырёхсторонника.

См. также

• Решение треугольников
• Теорема синусов
• Теоремы косинусов (сферическая геометрия)

Примечания

1. ↑ Приводится по изданию: Степанов Н.Н. Формулы синусов // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 29—32. — 154 с.

Литература

• Матвиевская Г. П. Очерки истории тригонометрии. Ташкент: Фан, 1990.

Для улучшения этой статьи по математике желательно?: Проставить интервики в рамках проекта Интервики. Добавить иллюстрации.