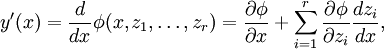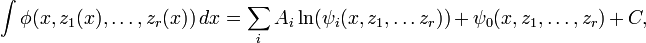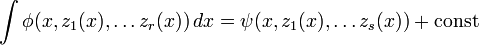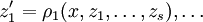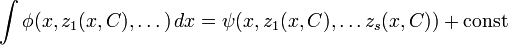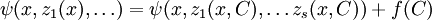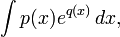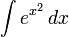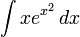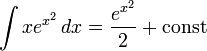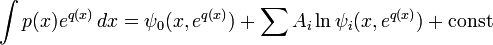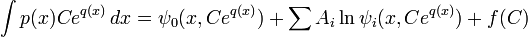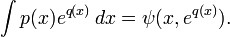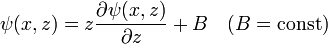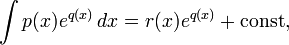Элементарная функция

Элементарные функции — функции, которые можно получить из основных элементарных функций:

• многочлен,
• рациональная,
• степенная,
• показательная и логарифмическая,
• тригонометрические и обратные тригонометрические
• Гиперболические функции

с помощью конечного числа арифметических действий и композиций. Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, отвечающих перечисленным операциям.

Элементарные функции по Лиувиллю

Рассматривая функции комплексного переменного, Лиувилль определил элементарные функции несколько шире. Элементарная функция y переменной x — аналитическая функция, которая может быть представлена как алгебраическая функция 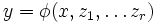$y=\phi(x,z_1,\dots z_r)$ от x и функций 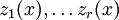$z_1(x), \dots z_r(x)$, причем $z_1 \dots z_r$ является логарифмом или экспонентой от некоторой алгебраической функции g₁ от x.

Например, sin(x) — алгебраическая функция от e^ix.

Не ограничивая общности рассмотрения, можно считать функции 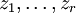$z_1, \dots, z_r$ алгебраически независимы, то есть если алгебраическое уравнение 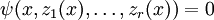$\psi(x,z_1(x), \dots, z_r(x))=0$ выполняется для всех x, то все коэффициенты полинома 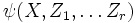$\psi(X,Z_1, \dots Z_r)$ равны нулю.

Дифференцирование элементарных функций

Элементарные функции непрерывны и бесконечно дифференцируемы всюду, где они определены. При этом производная элементарной функции всегда является элементарной функцией и может быть найдена за конечное число действий. Именно, по правилу дифференцирования сложной функции

$y'(x)=\frac{d}{dx}\phi(x,z_1, \dots, z_r)=\frac{\partial \phi}{\partial x} +\sum \limits_{i=1}^r\frac{\partial \phi}{\partial z_i}\frac{dz_i}{dx},$

где z₁'(z) равно или g₁' / g₁ или z₁g₁' в зависимости от того, логарифм ли z₁ или экспонента и т. д. На практике удобно использовать таблицу производных.

Интегрирование элементарных функций

Интеграл элементарной функции не всегда сам является элементарной функцией. Наиболее распространенные функции, интегралы которых найдены, собраны в таблице интегралов. В общем случае имеет место теорема:

Теорема Лиувилля. Если интеграл от элементарной функции 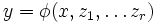$y=\phi(x,z_1, \dots z_r)$ сам является элементарной функцией, то он представим в виде

$\int \phi(x,z_1(x), \dots, z_r(x))\,dx= \sum \limits_i A_i \ln (\psi_i(x,z_1, \dots z_r)) + \psi_0(x,z_1, \dots, z_r) + C,$

где A_i — некоторые комплексные числа, а ψ_i — алгебраические функции своих аргументов.

Доказательство этой теоремы Лиувилль основал на следующем принципе. Если интеграл от y берется в элементарных функциях, то верно

$\int \phi(x, z_1(x), \dots z_r(x))\,dx =\psi(x, z_1(x), \dots z_s(x)) + \operatorname{const}$

где ψ — алгебраическая функция, z_{r + 1} — логарифм или экспонента алгебраической функции 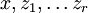$x,z_1, \dots z_r$ и т. д. Функции 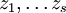$z_1, \dots z_s$ являются алгебраически независимыми и удовлетворяют некоторой системе дифференциальных уравнений вида

$z_1'=\rho_1(x,z_1, \dots, z_s), \dots$

где ρ_i — алгебраические функции своих аргументов. Если 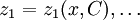$z_1=z_1(x,C), \dots$ — семейство решений этой системы, то

$\int \phi(x, z_1(x,C), \dots)\,dx = \psi(x, z_1(x, C), \dots z_s(x, C)) +\operatorname{const}$

откуда

$\psi(x, z_1(x), \dots) = \psi(x, z_1(x, C), \dots z_s(x, C)) +f(C)$

Для некоторых классов интегралов эта теорема позволяет весьма просто исследовать разрешимость в элементарных функциях задачи об интегрировании.

Интегрирование функций вида p(x)e^q(x)

Следствие теоремы Лиувилля (См. Ритт, с. 47 и сл.). Если интеграл

$\int p(x)e^{q(x)}\,dx,$

где p,q — полиномы, берется в элементарных функциях, то

$\int p(x)e^{q(x)}\,dx= r(x) e^{q(x)}$,

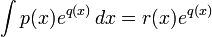где r(x) — тоже некоторый полином, удовлетворяющий дифференциальному уравнению

r' + q'(x)r = p(x)

Пример. В частности, интеграл

$\int e^{x^2}\,dx$

не берется, поскольку подстановка

$r=Ax^n+\dots \quad (A\not =0)$

в уравнение

r' + 2xr = 1

дает A = 0. Интеграл же

$\int xe^{x^2}\,dx$

берется, поскольку

r' + 2xr = x

имеет решение r = 1 / 2. При этом, конечно,

$\int xe^{x^2}\,dx=\frac{e^{x^2}}{2}+ \operatorname{const}$

Доказательство следствия. В силу теоремы Лиувилля

$\int p(x)e^{q(x)}\,dx= \psi_0(x, e^{q(x)}) + \sum A_i\ln \psi_i(x,e^{q(x)})+ \operatorname{const}$

Тогда в силу принципа Лиувилля при произвольной константе C верно

$\int p(x)C e^{q(x)}\,dx= \psi_0(x, Ce^{q(x)}) +\sum A_i\ln \psi_i(x,Ce^{q(x)})+ f(C)$

Дифференцируя по C и полагая C = 1, видим, что интеграл выражается алгебраически через x,e^q(x), то есть

$\int p(x)e^{q(x)}\,dx= \psi(x,e^{q(x)}).$

Опять применяя принцип Лиувилля, имеем

Cψ(x,e^q(x)) = ψ(x,Ce^q(x)) + f(C).

Дифференцируя по C и полагая C = 1, имеем

$\psi(x,z) = z \frac{\partial \psi(x,z)}{\partial z} + B \quad (B=\operatorname{const})$

при z = e^q(x), а следовательно, в силу алгебраической независимости x,e^q(x), при всех x,z. Поэтому

ψ(x,z) = − B + zr(x),

где r — некоторая алгебраическая функция x. Таким образом,

$\int p(x)e^{q(x)}\,dx = r(x)e^{q(x)} + \operatorname{const},$

Коль скоро сам интеграл заведомо является целой функций x, то r — полином. Следствие доказано.

Интегрирование алгебраических функций

Наиболее сложным оказался вопрос об интегрировании в элементарных функциях функций алгебраических, то есть о взятии абелевых интегралов, которому посвящены обширные исследования Вейерштрасса, Пташицкого^[1] и Риша^[2].

Теорема Лиувилля является основой для создания алгоритмов символьного интегрирования элементарных функций, реализуемых, напр., в

Вычисление пределов

Теория Лиувилля не распространяется на вычисление пределов. Не известно, существует ли алгоритм, который по заданной элементарной формулой последовательности дает ответ, имеет ли она предел или нет. Например, открыт вопрос о том, сходится ли последовательность 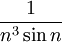$\frac{1}{n^3 \sin n}$.^[3]

См. также

• Дифференциальная теория Галуа

Литература

• J. Liouville. Mémoire sur l’intégration d’une classe de fonctions transcendantes // J. Reine Angew. Math. Bd. 13, p. 93-118. (1835)
• J.F. Ritt. Integration in Finite Terms. N.-Y., 1949// http://lib.homelinux.org
• А. Г. Хованский. Топологическая теория Галуа: разрешимость и неразрешимость уравнений в конечном виде Гл. 1. M, 2007

Примечания

1. ↑ Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. Art. 2 B 2 (W. Wirtinger, 1901 г.)
2. ↑ Дэвенпорт Дж. Интегрирование алгебраических функций. Гл. 4. М., «Мир», 1985
3. ↑ http://www.mccme.ru/ask/qa/pi_irr.html