Целые числа

Множество целых чисел 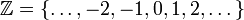$\mathbb{Z}=\{\dots,-2,-1,0,1,2,\dots\}$ определяется как замыкание множества натуральных чисел 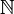$\mathbb{N}$ относительно арифметических операций сложения (+) и вычитания (-). Таким образом, сумма, разность и произведение двух целых чисел есть снова целые числа. Оно состоит из положительных натуральных чисел (1, 2, 3), чисел вида -n (n 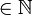$\in\mathbb{N}$ ) и числа нуль.

Необходимость рассмотрения целых чисел продиктована невозможностью (в общем случае) вычесть из одного натурального числа другое. Целые числа являются кольцом относительно операций сложения и умножения.

Отрицательные числа ввёл в математический обиход Михаэль Штифель (M. Stiffel), 1487—1567), в книге «Полная арифметика» 1544 года, и Никола Шюке (N. Chuquet, 1445—1500) — его работа была обнаружена в 1848 году.

Алгебраические свойства

$\mathbb{Z}$ не замкнуто относительно деления двух целых чисел (например, 1/2). Следующая таблица иллюстрирует несколько основных свойств сложения и умножения для любых целых a, b и c.

	сложение	умножение
замкнутость:	a + b — целое	a × b — целое
ассоциативность:	a + (b + c) = (a + b) + c	a × (b × c) = (a × b) × c
коммутативность:	a + b = b + a	a × b = b × a
существование нейтрального элемента:	a + 0 = a	a × 1 = a
существование противоположного элемента:	a + (−a) = 0	a × 1/a = 1
дистрибутивность умножения относительно сложения:	a × (b + c) = (a × b) + (a × c)

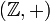На языке абстрактной алгебры первые пять вышеперечисленных свойств сложения говорят о том, что $\mathbb{Z}$ является абелевой группой относительно бинарной операции сложения, и, следовательно, также циклической группой, так как каждый ненулевой элемент $\mathbb{Z}$ может быть записан в виде конечной суммы 1 + 1 + … 1 или (−1) + (−1) + … + (−1). Фактически, $\mathbb{Z}$ является единственной бесконечной циклической группой по сложению в силу того, что любая бесконечная циклическая группа изоморфна группе $(\mathbb{Z},+)$ .

Первые четыре свойства умножения говорят о том, что $\mathbb{Z}$ — коммутативный моноид по умножению. Однако стоит заметить, что не каждое целое имеет противоположное по умножению, например, нет такого x из $\mathbb{Z}$ , что 2x = 1, так как левая часть уравнения четна, а правая нечетна. Из этого следует, что $\mathbb{Z}$ не является группой по умножению, а также не является полем. 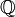Наименьшее поле, содержащее целые числа, — множество рациональных цисел ( $\mathbb{Q}$ ).

Совокупность всех свойств таблицы означает, что $\mathbb{Z}$ является коммутативным кольцом с единицей относительно сложения и умножения.

Обычное деление не определено на множестве целых чисел, но определено так называемое деление с остатком: для любых целых a и b, 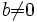$b \not= 0$ , существует единственный набор целых чисел q и r, что a = bq + r и 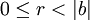$0 \le r &lt; |b|$ , где |b| — абсолютная величина (модуль) числа b. Здесь a — делимое, b — делитель, q — частное, r — остаток. На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел.

Теоретико-множественные свойства

$\mathbb{Z}$ — линейно упорядоченное множество без верхней и нижней границ. Порядок в нём задается соотношениями:

… < −2 < −1 < 0 < 1 < 2 < …

Целое число называется положительным, если оно больше нуля, отрицательным, если меньше нуля. Нуль не является положительным или отрицательным.

Для целых чисел справедливы следующие соотношения:

если a < b и c < d, тогда a + c < b + d.
если a < b и 0 < c, тогда ac < bc. (Отсюда легко показать, что если c < 0, то ac > bc.)