СЛУЧАЙНЫЙ ПРОЦЕСС

СЛУЧАЙНЫЙ ПРОЦЕСС

- ф-ция непрерывного времени 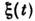,значение к-рой в каждый момент является случайной величиной, т. <е. величиной, подчиняющейся вероятностным законам. Если аргумент t изменяетсядискретно, то 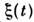наз. случайной последовательностью. Случайную ф-цию неск. непрерывных аргументов 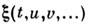называют переменным случайным полем. Примерами С. п. могут служитьразл. физ. процессы, сопровождающиеся случайными флуктуациями, а такжемн. процессы в геофизике, радиофизике, биофизике и др.

С. п. задан, если для любых моментов времени t₁,...,t_n известны многомерные (многоточечные) плотности вероятности 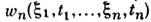для совокупности случайных величин либосоответствующие многомерные характеристические функции

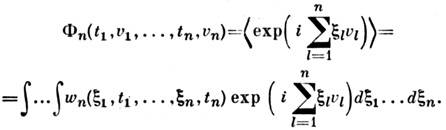
Для детерминиров. процессов 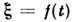плотность вероятности выражается через 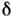-функцию, <напр.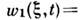

Исчерпывающей статистич. характеристикой С. п. является его характеристическийфункционал 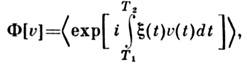где (...) означает статистич. усреднение по всевозможным реализациям С. <п. 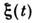наинтервале (T₁, T₂). Зная Ф[v], можно получить многомерныехарактеристич. ф-ции для 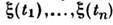, взяв в качестве аргумента функционала ф-цию 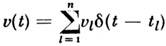. Коэф. разложения Ф[v] в окрестности v =0 определяют моментныефункции М _п С. п.: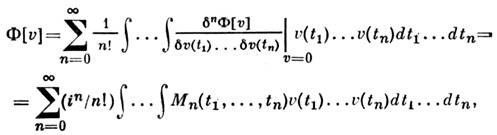

а коэф. разложения 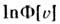- кумулянтные функции К _п: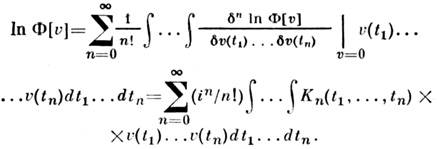

Кумулянтные ф-ции 1-го и 2-го порядка характеризуют ср. значение 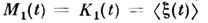и корреляционную функцию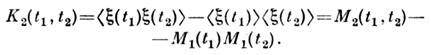

Ф-ции M_n(t₁,...,t_n )и K_n(t₁,...,t_n )при t₁ = t₂ = ...= t_n определяютодноточечные моменты и кумулянты С. ц.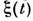, в частности со. интенсивность 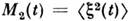, дисперсию 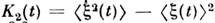,коэф. асимметрии 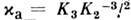и эксцесса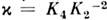

При ограниченных сведениях о С. п. либо при невозможности его полногоописания часто пользуются корреляционной теорией, рассматривающейтолько одноточечные и двухточечные статистич. характеристики 1-го и 2-гопорядка.

Вместо характеристич. функционала иногда используют функционал плотностивероятности С. п.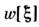, к-рый является континуальным аналогом многоточечной плотности вероятностии характеризует плотность вероятности отд. реализаций С. п.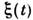.Нормировочный множитель функционала 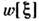обычно обращается в О или в 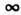,но это не препятствует использованию 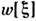при нахождении моментов и кумулянтов С. п., наиб. вероятных реализацийС. п. и т. п.

Перечисленные статистич. характеристики обобщают на комплексные и векторные(многомерные, многокомпонентные) С. п.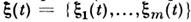. Наряду с моментами и кумулянтами, характеризующими статистич. свойстваотд. компонент С. п., пользуются также смешанными моментами и кумулянтами, <описывающими взаимные статистич. связи между компонентами С. п.

Нек-рые классы С. п. представляют спец. интерес для физики.

Стационарные процессы. С. п. наз. стационарным в узком смысле, есливсе его многоточечные вероятностные характеристики не меняются при измененииначала отсчёта времени, т. е. зависят только от разностей I; - tj. Еслиэтим свойством обладают только ср. значение и корреляц. ф-ция, т. е.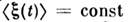и 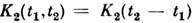, причём 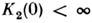,то С. п. является стационарным в широком смысле. Для стационарных в широкомсмысле процессов имеет место Винера - Хинчина теорема: корреляц. <ф-ция и спектральная плотность (спектр мощности) С. п. связаны друг с другомпреобразованием Фурье.

Время корреляции t _с, в течение к-рого корреляц. ф-ция спадаетв е раз, и ширина спектра 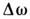связаны соотношением неопределённост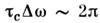и . При 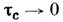величина 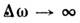и С. п. представляет собой белый шум.

Квазистационарные процессы. Если зависимость многоточечных статистич. <характеристик С. п. от положения на оси времени является медленной по сравнениюс зависимостью от разностей t_i - t_j, тотакой С. п. относят к классу квазистационарных. Для него можно ввести понятиемгновенной спектральной плотности.

Периодически - нестационарные процессы. У таких С. п. статистич. характеристикипериодически зависят от времени, напр. , где F(t) - периодич. детерминированная 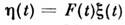ф-ция, а 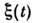- стационарный С. п.

Случайные процессы со стационарными п р и р а щ е н и я м и. Это процессы, <для к-рых, как и для стационарных процессов, сохраняется понятие спектральнойплотности, но коррсляц. ф-ция может и но существовать. Для статистич. описаниятаких С. п. пользуются не корреляционной, а структурно н функцией 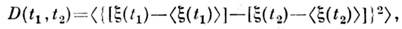равной дисперсии случайных приращений процесса на интервале (t₁,t₂). Структурная ф-ция стационарного процесса связана с его корреляц. ф-цией(если последняя существует) соотношением: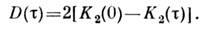

Гауссовы процессы. В случае нормальных (гауссовых) процессовмоментные и кумулянтные ф-ции произвольного порядка выражаются через ср. <значение и корреляц. ф-цию, к-рые дают, т. о., полное описание С. п. этогокласса. Значит. роль гауссовых процессов в физике определяется тем, чтоони реализуются практически всюду, где происходит сложение многих С. н.( центральная предельная теорема). Однородный гауссов процесс с независимымиприращениями наз. винеровским случайным процессом, служит непрерывноймоделью броуновского движения.

Марковские процессы (процессы без последействия), для них многоточечныевероятности выражаются через одномерные плотности распределения и двухточечныеплотности вероятности перехода.

Кроме того, выделяют ещё импульсные процессы, диффузионные процессы, <ветвящиеся процессы и др. Широкий класс С. п. составляют процессы, подчиняющиеся стохастическим уравнениям. Трудности в интерпретации эмпирич. статистич. <характеристик реальных процессов связаны с выделением статистич. ансамбля, <к к-рому может принадлежать ограниченный отрезок наблюдаемого процесса. <При выборе статистич. ансамбля фундам. роль играет эргодическая гипотеза, согласно к-рой моменты гипотетич. ансамбля отождествляют со среднимипо времени.

Лит.: Гнеденко Б. В., Курс теории вероятностей, 6 изд., М., 1988;Введение в статистическую радиофизику, ч. 1- Р ы т о в С. М., Случайныепроцессы, М., 1976; Справочник по теории вероятностей и математическойстатистике, 2 изд., М., 1985; Я г л о м А. М., Корреляционная теория стационарныхслучайных функций, Л., 1981; Розанов Ю. А., Теория вероятностей, случайныепроцессы и математическая статистика, М., 1985. О. В. Тулинский, Ю. <Л. Кравцов, А. Б. Шмелёв.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.