- ВЫПУКЛАЯ ФУНКЦИЯ
комплексного переменногог- регулярная однолистная функция

в единичном круге
 , отображающая единичный круг на нек-рую выпуклую область. Регулярная однолистная функция
, отображающая единичный круг на нек-рую выпуклую область. Регулярная однолистная функция 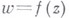 является В. ф. тогда и только тогда, когда при обходе любой окружности
является В. ф. тогда и только тогда, когда при обходе любой окружности 
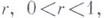 касательная к образу
касательная к образу  в точке
в точке  вращается в одном и том же направлении. Следующее неравенство выражает необходимое и достаточное условно выпуклости
вращается в одном и том же направлении. Следующее неравенство выражает необходимое и достаточное условно выпуклости  :
:

С другой стороны, для того чтобы
 была В. ф., необходимо и достаточно, чтобы она допускала следующее параметрич. представление:
была В. ф., необходимо и достаточно, чтобы она допускала следующее параметрич. представление:

где
 - неубывающая действительная функция па отрезке
- неубывающая действительная функция па отрезке  такая, что
такая, что

 - комплексные постоянные,
- комплексные постоянные,  Формулу (2) можно рассматривать как обобщение Кристоффеля - Шварца формулы для отображения круга Ена выпуклые многоугольники.
Формулу (2) можно рассматривать как обобщение Кристоффеля - Шварца формулы для отображения круга Ена выпуклые многоугольники.
Пусть
 - класс всех В. ф. в Е, нормированных условиями
- класс всех В. ф. в Е, нормированных условиями  суть подклассы класса
суть подклассы класса  , состоящие из функций, отображающих Есоответственно на выпуклые области плоскости wс р-кратной симметрией вращения относительно точки
, состоящие из функций, отображающих Есоответственно на выпуклые области плоскости wс р-кратной симметрией вращения относительно точки  Классы
Классы  компактны в себе относительно равномерной сходимости внутри Е. Их интегральные представления, в частности формула (2) для
компактны в себе относительно равномерной сходимости внутри Е. Их интегральные представления, в частности формула (2) для  , позволяют развить вариационные методы решения экстремальных задач на классах
, позволяют развить вариационные методы решения экстремальных задач на классах 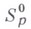 (см. [2] - [5]).
(см. [2] - [5]).
Основные экстремальные свойства класса
 характеризуются следующими неулучшаемыми неравенствами:
характеризуются следующими неулучшаемыми неравенствами:
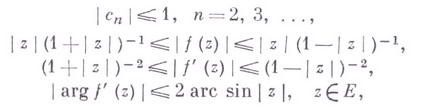
под аргументом функции понимается ветвь, обращающаяся в нуль при
 . Во всех этих оценках знак равенства имеет место только для функции'
. Во всех этих оценках знак равенства имеет место только для функции'
 . Для отношения
. Для отношения  кривизны
кривизны 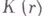 границы
границы  области
области  на классе
на классе 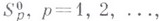 в точке
в точке  к кривизне
к кривизне 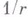 прообраза
прообраза 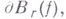 т. е. окружности
т. е. окружности 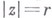 , в точке z имеются также неулучшаемые оценки. Областям
, в точке z имеются также неулучшаемые оценки. Областям  , принадлежит круг
, принадлежит круг  причем радиус этого круга не. может быть увеличен без дополнительных ограничений на класс функций. Если
причем радиус этого круга не. может быть увеличен без дополнительных ограничений на класс функций. Если 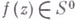 , то однолистная функция
, то однолистная функция  звездообразна в круге Е, т. е. отображает Ена область, звездную относительно начала координат.
звездообразна в круге Е, т. е. отображает Ена область, звездную относительно начала координат.
Примерами обобщения и видоизменения класса
 и его подклассов являются: класс
и его подклассов являются: класс  однолистных в
однолистных в  функций
функций  регулярных при
регулярных при 
 и отображающих
и отображающих  на области с выпуклыми дополнениями; класс
на области с выпуклыми дополнениями; класс  регулярных в кольце
регулярных в кольце  нормированных определенным образом функций
нормированных определенным образом функций  , каждая из к-рых однолистно отображает это кольцо в такую область, что конечная компонента ее дополнения выпукла и ее объединение с этой компонентой также выпукло; класс
, каждая из к-рых однолистно отображает это кольцо в такую область, что конечная компонента ее дополнения выпукла и ее объединение с этой компонентой также выпукло; класс  функций из
функций из  с действительными коэффициентами разложений Тейлора в окрестности точки
с действительными коэффициентами разложений Тейлора в окрестности точки  . Понятие В. ф. распространяется и на многолистные функции (см. [2], добавление).
. Понятие В. ф. распространяется и на многолистные функции (см. [2], добавление).
Самостоятельный интерес представляет следующее обобщение В. ф. (см. [6]): регулярная в круге Ефункция
 наз. близкой к выпуклой, если существует в ЕВ. ф.
наз. близкой к выпуклой, если существует в ЕВ. ф. такая, что всюду в Е
такая, что всюду в Е

Для класса Квсех таких функций f(z) доказана однолистность, найдены необходимые и достаточные условия принадлежности функции f(z) классу Ки параметрич. представление функций
 при помощи интегралов Стилтьеса:
при помощи интегралов Стилтьеса:
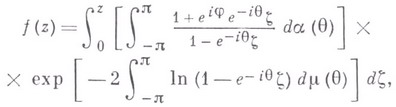
где
 - неубывающие действительные функции,
- неубывающие действительные функции,

Класс Квключает в себя выпуклые, звездные и другие функции. Для функций
 справедлива Бибербаха гипотеза:
справедлива Бибербаха гипотеза:  известны неулучшаемые оценки:
известны неулучшаемые оценки:

под аргументом функции понимается ветвь, обращающаяся в нуль при
 . Во всех этих оценках знак равенства имеет место только для функции
. Во всех этих оценках знак равенства имеет место только для функции 
 . Геометрически функции
. Геометрически функции  класса Кхарактеризуются тем, что они отображают круг Ена области D(f), внешность к-рых
класса Кхарактеризуются тем, что они отображают круг Ена области D(f), внешность к-рых  может быть заполнена лучами L, проведенными из точек границы области,
может быть заполнена лучами L, проведенными из точек границы области, 
 Понятие функции, близкой к выпуклой, распространено на многолистные функции (см. [7]).
Понятие функции, близкой к выпуклой, распространено на многолистные функции (см. [7]).
Лит.:[1] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [2] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [3] 3морович В. А., "Укр. матем. ж.", 1952, т. 4, с. 276-98; [4] Александров И. А., Черников В. В., "Сиб. матем. ж.", 1963, т. 4, № 2, с. 261 - 67; [5] 3морович В. А., "Матем. сб.", 1953, т. 32, № 3, с. 633-52; [6] Кар1an W., (.Michigan Math, J.", 1952, v. 1, № 2, p. 169-85; [7] Styer D., "Trans. Amer. Math. Soc.", 1972, v. 169, p. 105-12. И. А. Александров, Ю. <Д. <Максимов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
