ВНЕШНЯЯ И ВНУТРЕННЯЯ КРАЕВЫЕ ЗАДАЧИ

краевые задачи (к. з.) для эллиптич. уравнений с частными производными соответственно в конечной (внутренней) D⁺ и бесконечной (внешней) D ^- областях, на к-рые данная замкнутая гладкая поверхность S, гомеоморфная сфере, разделяет евклидово пространство R.³.

Основное отличие внешней к. з. от внутренней состоит в том, что в ней необходимо дополнительно к краевому условию потребовать от решения определенного поведения на бесконечности, обеспечивающего единственность решения и являющегося естественным с точки зрения физического происхождения данной задачи.

Напр., в случае внешней к. з. для уравнения Пуассона (функция f предполагается достаточно гладкой и финитной) достаточно потребовать, чтобы решение и(М).было регулярным на бесконечности, т. е. чтобы

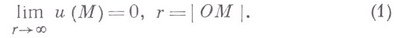
В случае внешней к. з. для уравнения Пуассона 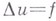в бесконечной плоской области условие регулярности на бесконечности сводится к требованию, чтобы решение и (М).было ограниченным на бесконечности: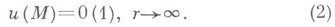

В случае внешней к. з. для уравнения Гельмгольца требование регулярности на бесконечности оказывается недостаточным для выделения единственного решения и применяется так наз. излучения условие. Для области в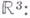

и для

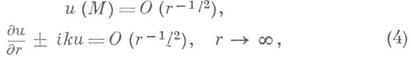
причем знаки здесь выбираются в зависимости от условий задачи и выбора главного фундаментального решения. О других условиях на бесконечности см. Предельного поглощения принцип, Предельной амплитуды принцип.

Пусть теперь рассматриваются к. з. для линейного эллиптич. уравнения общего вида

в областях и 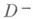евклидова пространства 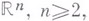выделяемых замкнутой гладкой гиперповерхностью S, гомеоморфной сфере в , причем функции с и f предполагаются достаточно гладкими, f - финитная. Условия регулярности на бесконечности типа (1) или (2) будут достаточны во внешних к. з. соответственно при или в тех случаях, когда для оператора Lвыполняется принцип максимума и существует одно единственное главное фундаментальное решение; в частности, для этого необходимо ; см. [1], [2], [3]. Вопрос о применимости условия излучения, принципа предельного поглощения и принципа предельной амплитуды в общем виде нельзя считать полностью изученным (1977).

Кроме условий на бесконечности, внешняя и внутренняя к. з. могут отличаться условиями существования решения. Напр., в случае внутренней Неймана задачи, для уравнения Лапласа 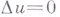в конечной области необходимое условие существования решения имеет вид

где 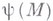- заданная граничная функция в условии Неймана . Однако для внешней задачи Неймана в бесконечной области это условие уже не является необходимым.

Лит.:[1] Смирнов В. И., Курс высшей математики, т. 4, 5 изд., М., 1958; [2] Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971 ;[3] Купрадзе В. Д., Граничные задачи теории колебаний и интегральные уравнения, М.-Л., 1950; [4] его же, Методы потенциала в теории, упругости, М., 1963; [5] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957. Е. Д. Соломенцев.