Конечнопорожденный идеал

Конечнопорождённым идеалом I ассоциативного кольца A назвается такой идеал, который порождается конечным числом своих элементов. Для одностороннего (например, правого) идеала это означает, что существует конечное множество элементов 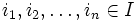$i_1, i_2, \ldots, i_n\in I$ таких, что любой элемент из I представим в виде суммы 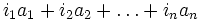$i_1a_1+i_2a_2+\ldots+i_na_n$, где $a_1, a_2, \ldots, a_n\in A$ — какие-то элементы кольца. Это определение полностью соответствует определению конечнопорождённого модуля над кольцом (если рассматривать правый идеал как правый модуль над кольцом A).

Двусторонний идеал называется конечнопорождённым, если существует конечное множество элементов 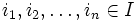$i_1, i_2, \ldots, i_n\in I$ таких, что любой элемент из I представим в виде суммы $a_1i_1b_1+a_2i_2b_2+\ldots+a_ni_nb_n$, где $a_1, a_2, \ldots, a_n\in A$ и $b_1, b_2, \ldots, b_n\in A$ — какие-то элементы кольца A.

См. также

• Идеал