- Конечнопорожденная абелева группа
-
В абстрактной алгебре абелева группа
 называется конечнопорождённой, если существует конечный набор
называется конечнопорождённой, если существует конечный набор  , такой что
, такой что  существует представление
существует представлениегде
 — целые числа. В таком случае говорится, что
— целые числа. В таком случае говорится, что  порождает множество
порождает множество  или что
или что  порождают
порождают  .
.Очевидно, каждая конечная абелева группа является конечнопорождённой. Конечнопорождённые абелевы группы имеют сравнительно простую структуру и могут быть полностью классифицированы.
Содержание
Примеры
- Целые числа
 являются конечнопорождённой абелевой группой.
являются конечнопорождённой абелевой группой. - Числа по модулю
 являются конечнопорождённой абелевой группой.
являются конечнопорождённой абелевой группой. - Любое прямое произведение конечного числа конечнопорождённых абелевых групп также является конечнопорождённой абелевой группой.
Нет других конечнопорождённых групп. Группа
 рациональных чисел не является конечнопорожденной: если
рациональных чисел не является конечнопорожденной: если  , возьмём натуральное число w взаимно простое ко всем их делителям; тогда 1 / w не может быть порождено
, возьмём натуральное число w взаимно простое ко всем их делителям; тогда 1 / w не может быть порождено  .
.Классификация
Теорема о классификации конечнопорожденных абелевых групп утверждает, что любая конечнопорождённая абелева группа
 изоморфна прямому произведению простых циклических групп и бесконечных циклических групп, где простая циклическая группа — это такая циклическая группа, чей порядок является степенью простого числа. Что значит, что каждая такая группа изоморфна группе вида
изоморфна прямому произведению простых циклических групп и бесконечных циклических групп, где простая циклическая группа — это такая циклическая группа, чей порядок является степенью простого числа. Что значит, что каждая такая группа изоморфна группе видагде
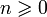 , и числа
, и числа  являются (не обязательно различными) степенями простых чисел. Значения
являются (не обязательно различными) степенями простых чисел. Значения  однозначно определены (с точностью до порядка) группой
однозначно определены (с точностью до порядка) группой  , в частности,
, в частности,  конечна тогда и только тогда, когда n = 0.
конечна тогда и только тогда, когда n = 0.На основании того факта что
 будет изоморфно произведению
будет изоморфно произведению  и
и  тогда и только тогда, когда j и k взаимно просты и m = jk, мы также можем представить любую конечнопорождённую группу
тогда и только тогда, когда j и k взаимно просты и m = jk, мы также можем представить любую конечнопорождённую группу  в форме прямого произведения
в форме прямого произведениягде k1 делит k2, который делит k3 и так далее до ku. И снова, числа n и
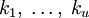 однозначно заданы группой
однозначно заданы группой  .
.См. также
Ссылки
Wikimedia Foundation. 2010.



