Конечно-разностная схема

Разностная схема — это конечная система алгебраических уравнений, поставленная в соответствие какой-либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия (например краевые условия и/или начальное распределение). Таким образом, разностные схемы применяются для сведения дифференциальной задачи, имеющей континуальный характер, к конечной системе уравнений, численное решение которых принципиально возможно на вычислительных машинах. Алгебраические уравнения, поставленные в соответствие дифференциальному уравнению получаются применением разностного метода, что отличает теорию разностных схем от других численных методов решения дифференциальных задач (например проекционных методов, таких как метод Галёркина).

Решение разностной схемы называется приближенным решением дифференциальной задачи.

Хотя формальное определение не накладывает существенных ограничений на вид алгебраических уравнений, но на практике имеет смысл рассматривать только те схемы, которые каким-либо образом отвечают дифференциальной задаче. Важными понятиями теории разностных схем являются понятия сходимости, аппроксимации, устойчивости, консервативности.

Аппроксимация

Для того чтобы уравнения были как-то связаны с приближаемым дифференциальным оператором нужно, чтобы уравнения удовлетворяли многочленам. Если уравнения выполняются для всех многочленов степени не выше r с точностью до 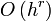$O\left(h^r\right)$ (буквой h принято обозначать шаг сетки), то говорят, что разностная схема имеет r-тый порядок аппроксимации.

Устойчивость

Условия аппроксимации не достаточно для того, чтобы результат разностной схемы приближался к точному ответу при h→0. В случае схем, коэффициенты которых не зависят от решения дифференциального уравнения, нужно выполнение условия устойчивости. Такие схемы можно представить как некоторый линейный оператор, который преобразует значения функции в момент t в значения функции в момент t+h. Условие устойчивости требует, чтобы собственные числа (вообще говоря комплексные) этого оператора не превосходили по модулю 1+ch, где с — некоторая константа, при h→0. Если это условие не выполнено, то погрешности схемы быстро возрастают и результат тем хуже, чем меньше шаг. Если выполнены как условие аппроксимации, так и условие устойчивости, то результат разностной схемы сходится к решению дифференциального уравнения (теорема Лакса-Рябенького)

Условие Куранта

Условие Куранта (в англоязычной литературе англ. Courant-Friedrichs-Levy condition, CFL) — скорость распространения возмущений в разностной задаче не должна быть меньше, чем в дифференциальной. Если это условие не выполнено, то результат разностной схемы может не стремится к решению дифференциального уравнения. Другими словами, за один шаг по времени частица не должна «пробегать» более одной ячейки.

В случае схем, коэффициенты которых не зависят от решения дифференциального уравнения, условие Куранта следует из устойчивости.

Для гиперболических систем уравнений это условие часто имеет вид

$\tau \le \min\left(\frac{h}{|\lambda|_{max}}\right)$

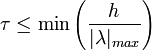
(τ — шаг по времени, h — шаг пространственной сетки, | λ | _max — максимальное по модулю собственное значение в точке. Минимум берется по всем точкам сетки.)

Классификация схем

Явные схемы

Явные схемы вычисляют значение результата через несколько соседних точек данных. Пример явной схемы для дифференцирования: 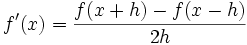$f'(x)=\frac{f(x+h)-f(x-h)}{2h}$ (2-й порядок аппроксимации). Явные схемы часто оказываются неустойчивыми.

Согласно теореме Годунова среди линейных разностных схем для уравнения переноса с порядком аппроксимации выше первого нет устойчивых. Таким образом, все устойчивые схемы высокого порядка аппроксимации являются нелинейными (несмотря на линейность исходного уравнения).

Неявные схемы

Неявные схемы используют уравнения, которые выражают данные через несколько соседних точек результата. Для нахождения результата решается система линейных уравнений. Пример неявной схемы для уравнения струны: f(x,t + h) − 2f(x,t) + f(x,t − h) = f(x + h,t + h) − 2f(x,t + h) + f(x − h,t + h). Неявные схемы обычно являются устойчивыми.

Полунеявные схемы

На одних шагах применяется явная схема, на других — неявная (как правило, эти шаги чередуются).
Пример(?) — Схема Кранка-Никольсо́на, когда решение берется в виде среднего от явной и неявной схемы решения для повышения точности

Компактные схемы

Компактные схемы используют уравнения, которые связывают значения результата в нескольких соседних точках с значениями данных в нескольких соседних точках. Это позволяет повысить порядок аппроксимации. Пример компактной схемы для дифференцирования: 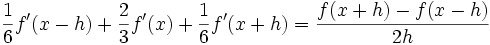$\frac{1}{6}f'(x-h)+\frac{2}{3}f'(x)+\frac{1}{6}f'(x+h)=\frac{f(x+h)-f(x-h)}{2h}$ (4-тый порядок аппроксимации).

Консервативные схемы

Когда разностная схема удовлетворяет тем же интегральным соотношениям (например, сохранению энергии, энтропии), что и первоначальное дифференциальное уравнение, то говорят о свойстве консервативности. Консервативные схемы обычно представляются в дивергентном виде.

Примеры консервативных схем гидродинамики — схема Самарского, метод крупных частиц Белоцерковского.

Схемы на смещенных сетках

В этих схемах сетки, на которых задан результат, и данные смещены относительно друг друга. Например, точки результата находятся посередине между точками данных. В некоторых случаях это позволяет использовать более простые граничные условия.

См. также

• Метод конечных разностей
• Метод конечных разностей во временной области
• Численное интегрирование

Ссылки

• «Разностные схемы» — Глава в wikibooks на тему «Разностные схемы для гиперболических уравнений»
• [1] Демьянов А. Ю., Чижиков Д. В. Неявная гибридная монотонная разностная схема второго порядка точности