- Квадратурные формулы
-
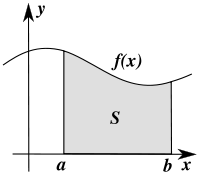 Определённый интеграл как площадь фигуры
Определённый интеграл как площадь фигурыЧисленное интегрирование (историческое название: квадратура) — вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком интегрируемой функции и отрезками прямых
 и
и 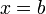 , где
, где 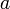 и
и 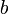 — пределы интегрирования (см. рисунок).
— пределы интегрирования (см. рисунок).Необходимость применения численного интегрирования чаще всего может быть вызвана отсутствием у первообразной функции представления в элементарных функциях и, следовательно, невозможностью аналитического вычисления значения определённого интеграла по формуле Ньютона-Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.
Содержание
Одномерный случай
Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При этом для оценки значения интеграла получаются формулы вида
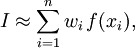
где
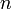 — число точек, в которых вычисляется значение подынтегральной функции. Точки
— число точек, в которых вычисляется значение подынтегральной функции. Точки 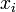 называются узлами метода, числа
называются узлами метода, числа 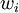 — весами узлов. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона). Часто формулы для оценки значения интеграла называют квадратурными формулами.
— весами узлов. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона). Часто формулы для оценки значения интеграла называют квадратурными формулами.Метод прямоугольников
Пусть требуется определить значение интеграла функции на отрезке
![\left[ {a},{b} \right]](/pictures/wiki/files/55/7096f612f66dfff84bc01965eea1fbf8.png) . Этот отрезок делится точками
. Этот отрезок делится точками 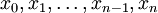 на
на 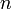 равных отрезков длиной
равных отрезков длиной 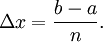 Обозначим через
Обозначим через 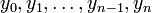 значение функции
значение функции 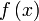 в точках
в точках 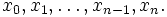 Далее составляем суммы
Далее составляем суммы 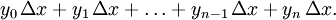 Каждая из сумм — интегральная сумма для
Каждая из сумм — интегральная сумма для 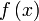 на
на ![\left[ {a},{b} \right]](/pictures/wiki/files/55/7096f612f66dfff84bc01965eea1fbf8.png) и поэтому приближённо выражает интеграл
и поэтому приближённо выражает интеграл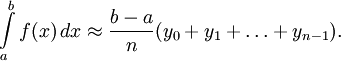
Если заданная функция — положительная и возрастающая, то эта формула выражает площадь ступенчатой фигуры, составленной из «входящих» прямоугольников, а формула
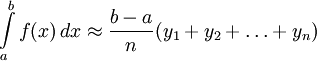
выражает площадь ступенчатой фигуры, состоящей из «выходящих» прямоугольников. Чем меньше длина отрезков, на которые делится отрезок
![\left[ {a},{b} \right]](/pictures/wiki/files/55/7096f612f66dfff84bc01965eea1fbf8.png) , тем точнее значение, вычисляемое по этой формуле, искомого интеграла.
, тем точнее значение, вычисляемое по этой формуле, искомого интеграла.Метод трапеций
Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций.
Площадь трапеции на каждом отрезке:
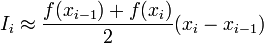
Погрешность аппроксимации на каждом отрезке:
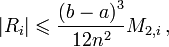 где
где ![M_{2,i}=\max_{x\mathcal{2}[x_{i-1},x_i]} \left| f''(x) \right|](/pictures/wiki/files/55/751bcc3b31bb41b88c1e5123348475ea.png)
Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины h:
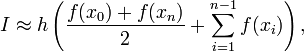 где
где 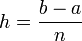
Погрешность формулы трапеций:
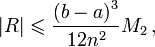 где
где ![M_{2}=\max_{x\mathcal{2}[a,b]} \left| f''(x) \right|](/pictures/wiki/files/52/4f29816d6ff0cc7160ca6fb88300f447.png)
Метод парабол (метод Симпсона)
Использовав три точки отрезка интегрирования можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид
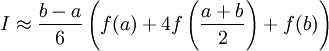 .
.Если разбить интервал интегрирования на 2N равных частей, то имеем
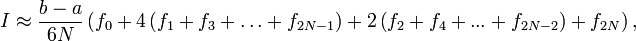
где
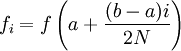 .
.Увеличение точности
Приближение функции одним полиномом на всем отрезке интегрирования, как правило, приводит к большой ошибке в оценке значения интеграла.
Для уменьшения погрешности отрезок интегрирования разбивают на части и применяют численный метод для оценки интеграла на каждой из них.
При стремлении количества разбиений к бесконечности, оценка интеграла стремится к его истинному значению для аналитических функций для любого численного метода.
Приведённые выше методы допускают простую процедуру уменьшения шага в два раза, при этом на каждом шаге требуется вычислять значения функции только во вновь добавленных узлах. Для оценки погрешности вычислений используется правило Рунге.
Метод Гаусса
Описанные выше методы используют фиксированные точки отрезка (концы и середину) и имеют низкий порядок точности (0 - методы правых и левых прямоугольников, 1 - методы средних прямоугольников и трапеций, 3 - метод парабол (Симпсона)). Если мы можем выбирать точки, в которых мы вычисляем значения функции f(x), то можно при том же количестве вычислений подынтегральной функции получить методы более высокого порядка точности. Так для двух (как в методе трапеций) вычислений значений подынтегральной функции, можно получить метод уже не 1-го, а 3-го порядка точности:
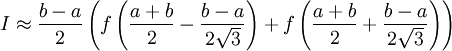 .
.
В общем случае, используя n точек, можно получить метод с порядком точности 2n − 1. Значения узлов метода Гаусса по n точкам являются корнями полинома Лежандра степени n.
Значения узлов метода Гаусса и их весов приводятся в справочниках специальных функций. Наиболее известен метод Гаусса по пяти точкам.
Метод Гаусса-Кронрода
Недостаток метода Гаусса состоит в том, что он не имеет лёгкого (с вычислительной точки зрения) пути оценки погрешности полученного значения интеграла. Использование правила Рунге требует вычисления подынтегральной функции примерно в таком же числе точек, не давая при этом практически никакого выигрыша точности, в отличие от простых методов, где точность увеличивается в несколько раз при каждом новом разбиении. Кронродом был предложен следующий метод оценки значения интеграла
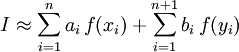 ,
,
где xi — узлы метода Гаусса по n точкам, а 3n + 2 параметров ai, bi, yi подобраны таким образом, чтобы порядок точности метода был равен 3n + 1.
Тогда для оценки погрешности можно использовать эмпирическую формулу:
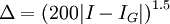 ,
,
где IG — приближённое значение интеграла, полученное методом Гаусса по n точкам. Библиотеки gsl и SLATEC для вычисления определённых интегралов содержат подпрограммы, использующие метод Гаусса-Кронрода по 15, 21, 31, 41, 51 и 61 точкам.
Метод Чебышёва
Интегрирование при бесконечных пределах
Для интегрирования по бесконечным пределам нужно ввести неравномерную сетку, шаги которой нарастают при стремлении к бесконечности, либо можно сделать такую замену переменных в интеграле, после которой пределы будут конечны. Аналогичным образом можно поступить, если функция особая на концах отрезка интегрирования
См. в том числе Метод Самокиша
Методы Монте-Карло
Методы Рунге-Кутты
Многомерный случай
В небольших размерностях можно так же применять квадратурные формулы, основанные на многочленах Лагранжа. Однако в больших размерностях эти методы становятся неприемлемыми из-за быстрого возрастания числа точек сетки и/или сложной границы области. В этом случае применяется метод Монте-Карло. Генерируются случайные точки в нашей области и усредняются значения функции в них. Так же можно использовать смешанный подход — разбить область на несколько частей, в каждой из которых (или только в тех, где интеграл посчитать не удаётся из-за сложной границы) применить метод Монте-Карло.
Литература
ISBN 5-03-003392-0 Д.Каханер, К.Моулер, С.Нэш. Численные методы и программное обеспечение (пер. с англ.). М.: Мир, 2001, 575 c.
ISBN 5-02-013996-3 Самарский А. А., Гулин А. В. Численные методы: Учеб. пособие для вузов. — М.: Наука. Гл. ред. физ-мат. лит., 1989. — 432 с.
Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов.-13-е изд.-М.: Наука. Гл. ред. физ-мат. лит., 1985. — 432 с.
Wikimedia Foundation. 2010.
