Квадрат (степень)

y=x², при целых значениях x на отрезке от 1 до 25

Квадра́том числа называется результат умножения числа на само себя (возведения числа в степень 2).

Далее приведено начало числовой последовательности для квадратов целых неотрицательных чисел (последовательность A000290 в OEIS):

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849...

Квадрат натурального числа n можно также представить в виде суммы первых n нечетных чисел:

1: 1 = 1

2: 4 = 1 + 3

...

7: 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13

...

Ещё один способ представления квадрата натурального числа:
n² = 1 + 1 + 2 + 2 + ... + (n − 1) + (n − 1) + n
Пример:

1: 1 = 1

2: 4 = 1 + 1 + 2

...

4: 16 = 1 + 1 + 2 + 2 + 3 + 3 + 4

...

Сумма квадратов первых n натуральных чисел вычисляется по формуле: $\sum_{i=1}^n i^2 = 1^2 + 2^2 + 3^2 + ... + n^2 = \frac {n(n + 1)(2n + 1)} {6}$

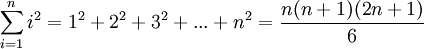
Геометрический смысл

Квадрат числа равен площади квадрата со стороной, равной этому числу.

См. также

• Взятие квадратного корня — обратная операция по отношению к возведению в квадрат.
• Куб