- Инъективное отображение
-
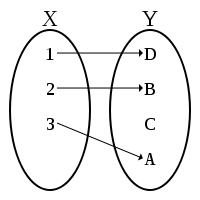 Инъективная функция.
Инъективная функция.Отображение
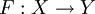 называется инъекцией (или вложением, или взаимно однозначным отображением в множество Y), если разные элементы множества X переводятся в разные элементы множества Y.
называется инъекцией (или вложением, или взаимно однозначным отображением в множество Y), если разные элементы множества X переводятся в разные элементы множества Y.Формально это значит, что если два образа совпадают, то совпадают и прообразы (
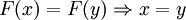 ). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью).
). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью).Инъекцию можно также определить как отображение, для которого существует левое обратное, то есть
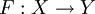 инъективно, если существует
инъективно, если существует 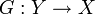 такое, что
такое, что 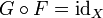 .
.Примеры
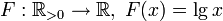 — инъективно.
— инъективно.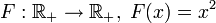 — инъективно.
— инъективно.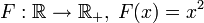 — не является инъективным (F( - 2) = F(2) = 4).
— не является инъективным (F( - 2) = F(2) = 4).
См. также
Литература
- Н. К. Верещагин, А.Шень. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств.
- Ершов Ю. Л., Палютин Е. А. Математическая логика: Учебное пособие. — 3-е, стереотип. изд. — СПб.: «Лань», 2004—336 с.
Wikimedia Foundation. 2010.
