- Звезда (геометрическая фигура)
-
 Правильная четырёхконечная звезда
Правильная четырёхконечная звездаЗвезда — определённый вид плоских невыпуклых многоугольников, не имеющий однако однозначного математического определения. Обычно под звёздами подразумевают фигуры, напоминающие по форме изображение звезды.
Одно из определений
Звезда — плоская геометрическая фигура, составленная из треугольных лучей, исходящих из общего центра, сливающихся в точке схождения.
По количеству лучей выделяют трёхконечные, четырёхконечные и т. д. звёзды.
Произвольная n-конечная звезда строится следующим образом: строится окружность. (Назовём отрезок, пересекающий эту окружность не более чем в одной точке, «внешним».) На ней произвольным образом выбирают n точек (назовём их «синими»). Далее вне круга, ограниченного этой окружностью, ставятся n точек (назовём их «красными») так, чтобы любая синяя точка была соединена внешними отрезками ровно с двумя красными, а любая красная точка была соединена двумя внешними отрезками ровно с двумя синими; при этом никакие два из этих отрезков не должны пересекаться иначе как в концах; и углы между двумя отрезками, исходящими из одной синей точки, — внешние углы звезды, — должны быть тупыми (следовательно, углы между двумя отрезками, исходящими из одной красной точки, — внутренние углы звезды, — должны быть острыми).
Звездой будет называться многоугольник, образованный построенными нами внешними отрезками. Очевидно, n-конечная звезда является невыпуклым 2n-угольником. Можно определить n-конечную звезду как 2n-угольник, у которого углы при вершинах поочерёдно то больше 180°, то меньше.
Окружность, на которой строилась звезда, называется базовой; базовая окружность входит в звезду; радиус базовой окружности является важной характеристикой звезды.
Правильной называется звезда, у которой все внутренние углы равны и все внешние углы равны.
Фигура, ограниченная двумя отрезками, исходящими из одной красной точки, и дугой базовой окружности, на которую этот угол опирается, называется лучом звезды. Очевидно:
- количество лучей равно угольности звезды (поэтому иногда n-конечную звезду называют n-лучевой);
- звезда суть объединение лучей с базовой окружностью;
- у правильной звезды прямые стороны всех лучей равны. (Звезду, у которой у каждого луча прямые стороны равны, но прямая сторона одного луча не обязательно равна прямой стороне другого луча, называют полуправильной; правильная звезда — частный вид полуправильной.)
Отрезки, соединяющие центр базовой окружности и красные точки, называются радиалами соответствующих данным красным точкам лучам звезды. Звезда, у которой длины всех радиалов равны, называется равнолучевой.
У полуправильной звезды углы между двумя соседними радиалами равны. У правильной звезды, кроме этого, длины радиалов равны. Таким образом, правильная звезда суть полуправильная равнолучевая звезда.
Другое определение
 Пятиконечная звезда {5/2}, вписанная в пятиугольник
Пятиконечная звезда {5/2}, вписанная в пятиугольникДругой вариант построения состоит в том что берётся одна окружность, на ней ставятся n точек и они соединяются между собой, при этом каждой точка соединяется с m-ой следующей точкой. Такая звезда обозначается символом {n/m}. При этом точки пересечения рёбер между собой внутри окружности не рассматриваются как вершины. Таким образом, такая звезда имеет n вершин и n рёбер, также как и правильный n-угольник.
Соотношение радиусов внешней (на которой лежат вершины углов лучей звезды) и внутренней (на которой лежат точки пересечения ребер соседних лучей) окружностей правильной звезды с вышеприведенным вариантом построения вычисляется по формуле
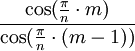 .
.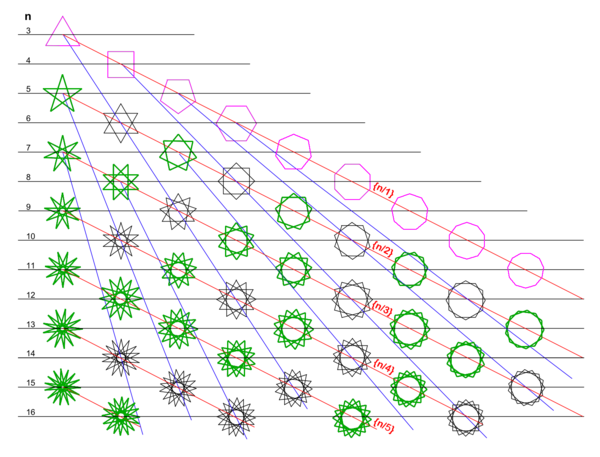 Двумерное дискретное можество звёзд.
Двумерное дискретное можество звёзд.
Фиолетовый - выпуклые многоугольники.
Зелёные - связанные звёзды ({n/m} где n и m взаимно простые числа).
Чёрные - не связанные звёзды ({n/m} где n и m не взаимно простые числа).См. также
Wikimedia Foundation. 2010.
