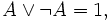- Закон исключения третьего
-
Закон исключённого третьего — закон классической логики, состоящий в том, что из двух высказываний — «А» или «не А» — одно обязательно является истинным, т.е. два суждения, одно из которых является отрицанием другого, не могут быть одновременно ложными, одно из них необходимо истинно. Закон исключённого третьего является одним из основополагающих принципов современной математики.
С интуиционистской (и, в частности, конструктивистской) точки зрения, установление истинности высказывания вида «А или не А» означает установление истинности A или истинности его отрицания,
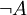 . Поскольку не существует общего метода, позволяющего для каждого высказывания за конечное число шагов установить его истинность или истинность его отрицания, закон исключенного третьего подвергается критике со стороны представителей интуиционистского и конструктивного направлений в основаниях математики.
. Поскольку не существует общего метода, позволяющего для каждого высказывания за конечное число шагов установить его истинность или истинность его отрицания, закон исключенного третьего подвергается критике со стороны представителей интуиционистского и конструктивного направлений в основаниях математики.Содержание
Формулировка
В математической логике закон исключенного третьего выражается формулой
где
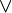 — знак дизъюнкции,
— знак дизъюнкции,  — знак отрицания.
— знак отрицания.Другие формулировки
Подобный смысл имеют другие логические законы, многие из которых сложились исторически. В частности, закон двойного отрицания и закон Пирса эквивалентны закону исключённого третьего в интуиционистской логике. Это означает, что расширение системы аксиом интуиционистской логики любым из этих трёх законов в любом случае приводит к классической логике. И все же, в общем случае, существуют логики, в которых все три закона неэквивалентны[1].
Примеры
Предположим, что P представляет собой утверждение «Сократ смертен». Тогда закон исключённого третьего для P примет вид: «Сократ смертен или Сократ бессмертен», откуда ясно, что закон отсекает все иные варианты, при которых Сократ и не смертен и не бессмертен. Последнее — это и есть то самое «третье», которое исключается. Этим также обусловлено латинское название данного закона: «лат. tertium non datur», то есть «третьего не дано».
Гораздо более тонкий пример применения закона исключённого третьего, который хорошо демонстрирует, почему он не является приемлемым с точки зрения интуиционизма, состоит в следующем. Предположим, что мы хотим доказать теорему, что существуют два таких иррациональных числа a и b, что ab рационально. Известно, что
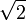 иррационально. Рассмотрим
иррационально. Рассмотрим 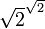 . Если данное число рационально, то теорема доказана. Иначе возьмём
. Если данное число рационально, то теорема доказана. Иначе возьмём 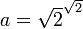 и
и 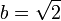 . Тогда
. Тогда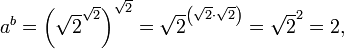
то есть рациональное число. По закону исключённого третьего иных вариантов быть не может. Поэтому, теорема в общем случае доказана. Причём доказательство предельно просто и элементарно. С другой стороны, если принять интуиционистскую точку зрения и отказаться от закона исключённого третьего, теорема хотя и может быть доказана, но доказательство её становится исключительно сложным.
Примечания
- ↑ Zena M. Ariola and Hugo Herbelin. Minimal classical logic and control operators. In Thirtieth International Colloquium on Automata, Languages and Programming , ICALP’03, Eindhoven, The Netherlands, June 30 — July 4, 2003, volume 2719 of Lecture Notes in Computer Science, pages 871—885. Springer-Verlag, 2003.[1]
Смотри также
Wikimedia Foundation. 2010.