Губка Мегера

Губка Менгера — геометрический фрактал, один из трёхмерных аналогов ковра Серпинского.

Построение

Куб K₀ с ребром 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из куба K₀ удаляются центральный куб и все прилежащие к нему по двумерным граням кубы этого подразделения. Получается множество K₁, состоящее из 20 оставшихся замкнутых кубов «первого ранга». Поступая точно так же с каждым из кубов первого ранга, получим множество K₂, состоящее из 400 кубов второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность

$K_0\supset K_1\supset\dots\supset K_n\supset\dots$

пересечение членов которой есть губка Менгера.

Свойства

• Губка Менгера имеет промежуточную (т. е. не целую) Хаусдорфову размерность, которая равна 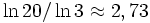$\ln20/\ln3\approx 2,73$ поскольку она состоит из 20 равных частей, каждая из которых подобна всей губке с коэффициентом подобия 1/3.
• Губка Менгера имеет топологическую размерность 1, более того
  • Губка Менгера топологически характеризуется как одномерный связный локально связный метризуемый компакт, не имеющий локально разбивающих точек (т. е. для любой связной окрестности U любой точки 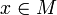$x\in M$ множество 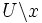$U\backslash x$ связно) и не имеющий непустых открытых и вложимых в плоскость подмножеств.
• Губка Менгера является универсальной кривой Урысона, то есть она обладает тем свойством, что какова бы ни была кривая Урысона C, в губке Менгера найдется подмножество C', гомеоморфное C.

См. также

• Кривая Урысона