Группа голономии

Параллельное перенесение вектора по замкнутому контуру на сфере. Угол α пропорционален площади внутри контура.

Параллельное перенесение — изоморфизм слоёв над концами кусочно гладкой кривой базы гладкого расслоения 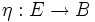$\eta:E\to B$, определяемый некоторой заданной связностью на E. В частности, линейный изоморфизм касательных пространств T_γ(0)(M) и T_γ(1)(M), определяемый вдоль кривой 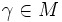$\gamma\in M$ некоторой заданной на M аффинной связностью.

Параллельное перенесение по аффинной связности

Пусть на гладком многообразии M задана аффинная связность. Говорят, что вектор 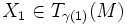$X_1\in T_{\gamma(1)}(M)$ получен параллельным перенесением из вектора 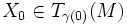$X_0\in T_{\gamma(0)}(M)$ вдоль не имеющей самопересечений гладкой кривой $\gamma:[0,1]\to M$, если в окрестности этой кривой существует гладкое векторное поле X со следующими свойствами:

• выполняются равенства X(γ(0)) = X₀ и X(γ(1)) = X₁;
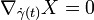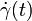• для любого значения $t\in [0,1]$ выполняется равенство $\nabla_{\dot\gamma(t)}X=0$, где символ $\nabla$ обозначает ковариантную производную, а $\dot\gamma(t)$ есть вектор скорости γ.

Замечание. Так как в локальных координатах справедливо равенство:

$(\nabla_{\dot\gamma}X)^i = \frac{d}{dt}X^i + \Gamma^i_{jk}X^j\dot\gamma^k$,

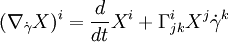и в этом выражении нет частных производных от компонент вектора X, в определении параллельного перенесения не обязательно требовать, чтобы векторное поле X было определено в целой окрестности пути γ(t), достаточно, чтобы оно существовало и было гладким вдоль одного только этого пути.

Параллельный перенос вдоль кусочно гладкой кривой (включая кривые с самопересечениями) определяется как суперпозиция параллельных переносов вдоль её не имеющих самопересечений гладких кусков.

На основе понятия параллельного переноса вектора определяются понятия параллельного переноса ковектора и тензора произвольной валентности.

Свойства параллельного перенесения векторов

• Согласно теории обыкновенных дифференциальных уравнений, решение задачи Коши произвольного линейного ОДУ продолжается неограниченно вдоль любой гладкой кривой, поэтому задавая вектор в начальной точке и указывая путь параллельного перенесения, этот вектор однозначно переносится в любую точку этого пути.
• При перенесении векторов вдоль одного и того же пути сохраняются все линейные соотношения между ними.
• Перенесение векторов обратимо: достаточно конечные вектора перенести вдоль обратного пути, чтобы получились исходные вектора.
• Как следствие двух предыдущих свойств получается, что оператор параллельного переноса вдоль кривой γ представляет собой линейный изоморфизм пространств T_γ(0)(M) и T_γ(1)(M).
• Если аффинная связность согласована с метрическим тензором на римановом многообразии (связность Леви-Чивита), тогда оператор параллельного перенесения является ортогональным, то есть сохраняет скалярные произведения векторов, их длины и углы между ними.
• Важным свойством параллельного перенесения является также независимость результата перенесения от параметризации пути (эквивалентные пути дадут одинаковый результат). В то же время параллельное перенесение вдоль различных кривых обычно приводит к различным результатам.

Связанные определения

• Геодезическая — гладкий путь, у которого касательный вектор в каждой точке получается параллельным перенесением касательного вектора из любой другой точки.
• Группа голономии — группа Φ_x автоморфизмов касательного пространства T_xM, определяемая параллельными переносом вдоль замкнутых кусочно гладких кривых. При этом, для связного многообразия Φ_x и Φ_y всегда сопряжены между собой.

История

Развитие понятия параллельного переноса началось с обычного параллелизма на евклидовой плоскости, для которой Миндинг в 1837 указал возможность обобщить её на случай поверхности в 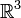$\R^3$ с помощью введенного им понятия развертывания кривой 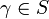$\gamma\in S$ на плоскость 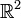$\R^2$. Это указание Миндинга послужило отправным пунктом для Леви-Чивиты, который, оформляя аналитически параллельный перенос касательного вектора на поверхности, обнаружил зависимость его только от метрики поверхности и на этой основе обобщил его сразу на случай n-мерного риманова пространства (см. связность Леви-Чивита). Дальнейшие обобщения этого понятия связаны с развитием общей теории связностей.

Литература

• Рашевский П. К. Риманова геометрия и тензорный анализ. — Любое издание.