Бета-функция Эйлера

Это статья о бета-функции Эйлера. См. также статью о бета-функции Дирихле.

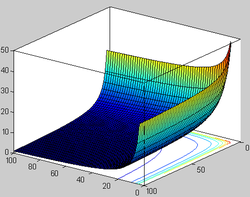
График бета-функции при вещественных аргументах

В математике бета-функцией (Β-функцией, бета-функцией Эйлера или интегралом Эйлера I рода) называется следующая специальная функция от двух переменных:

$\mathrm{\Beta}(x,y)=\int\limits_0^1t^{x-1}(1-t)^{y-1}\,dt$,

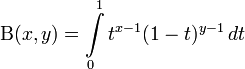определённая при $\Re(x)>0$, $\Re(y)>0$.

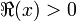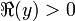Бета-функция была изучена Эйлером и Лежандром, а название ей дал Жак Бине.

Свойства

Бета-функция симметрична относительно перестановки переменных, то есть

Β(x,y) = Β(y,x).

Бета-функцию можно выразить через другие функции:

$\mathrm{\Beta}(x,\;y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$,

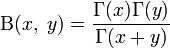где Γ(x) — Гамма-функция;

$\mathrm{\Beta}(x,\;y)=2\int\limits_0^{\pi/2}\sin^{2x-1}\theta\cos^{2y-1}\theta\,d\theta,\qquad\Re(x)>0,\ \Re(y)>0$;

$\mathrm{\Beta}(x,\;y)=\int\limits_0^\infty\frac{t^{x-1}}{(1+t)^{x+y}}\,dt,\qquad\Re(x)>0,\ \Re(y)>0$;

$\mathrm{\Beta}(x,\;y)=\frac{1}{y}\sum_{n=0}^\infty(-1)^n\frac{(y)_{n+1}}{n!(x+n)}$,

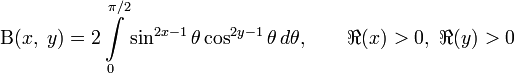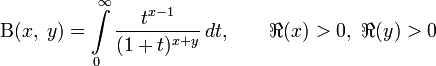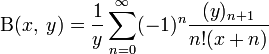где (x)_n — нисходящий факториал, равный $x\cdot(x-1)\cdot(x-2)\cdot\ldots\cdot(x-n+1)$.

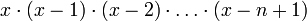Подобно тому как гамма-функция для целых чисел является обобщением факториала, бета-функция является обобщением биномиальных коэффициентов с немного изменёнными параметрами:

$\mathrm{C}_n^k = \frac1{(n+1)\Beta(n-k+1,\;k+1)}$.

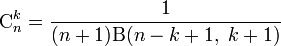Производные

Частные производные у бета-функции следующие:

${\partial\over\partial x}\Beta(x,\;y)=\Beta(x,\;y)\left( {\Gamma^\prime(x)\over\Gamma(x)}-{\Gamma^\prime(x+y)\over\Gamma(x+y)}\right)=\Beta(x,\;y)(\psi(x)-\psi(x+y))$,

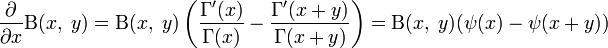где ψ(x) — дигамма-функция.

Неполная бета-функция

Неполная бета-функция — это обобщение бета-функции, заменяющее определённый интеграл неопределённым:

$\Beta_x(a,\;b)=\int\limits_0^x t^{a-1}\,(1-t)^{b-1}\,dt$.

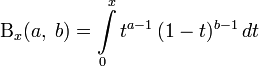При x = 1 неполная бета-функция совпадает с полной.

Регуляризованная неполная бета-функция определяется через полную и неполную бета-функции:

$I_x(a,\;b)=\frac{\Beta_x(a,\;b)}{\Beta(a,\;b)}$.

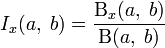Свойства I(x)

$I_0(a,\;b)=0$;

$I_1(a,\;b)=1$;

$I_x(a,\;b)=1-I_{1-x}(b,\;a)$.

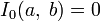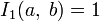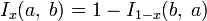Применение

С помощью бета-функции описываются многие свойства элементарных частиц, участвующих в сильном взаимодействии. Эта особенность подмечена Габриэле Венециано в 1968 году. В 1970 году Ёитиро Намбу, Холгер Бен Нильсен и Леонард Сасскинд сумели выявить физический смысл, скрывавшийся за бета-функцией. Это положило начало теории струн.

См. также

• Список объектов, названных в честь Леонарда Эйлера