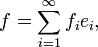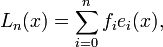- Бесконечномерное пространство
-
Ба́зис — множество векторов в линейном пространстве, таких, что любой вектор пространства может быть единственным образом представлен в виде их линейной комбинации.
Существуют две основных разновидности определения: базис Га́меля, и базис Ша́удера. Базис Га́меля применяется в основном в абстрактной алгебре (в частности в линейной алгебре). В функциональном анализе, в частности для гильбертова пространства, под базисом обычно понимается базис Ша́удера, понятие, основанное на разложении в ряды. В том случае, когда пространство имеет конечный базис (т.е. пространство конечномерно), обе этих разновидности совпадают.
Содержание
Базис Га́меля
Базис Га́меля (англ. Hamel basis) — множество векторов в линейном пространстве, таких, что любой вектор пространства может быть представлен в виде некоторой их конечной линейной комбинации (полнота базиса), при этом ни один из базисных векторов не представим в виде конечной линейной комбинации остальных (линейная независимость).
Свойства
- В каждом линейном пространстве существует базис (доказательство этой теоремы в общем случае неконструктивно и использует аксиому выбора).
- Базисами являются максимальные по включению линейно независимые системы векторов, и только они.
- Базисами являются минимальные по включению полные системы векторов, и только они.
- Единственная тривиальная (равная нулю) линейная комбинация векторов базиса возможна только при тривиальном наборе коэффициентов.
- Для любого вектора существует единственное представление в виде конечной линейной комбинации векторов базиса.
- Мощность базиса не зависит от выбора базисных векторов и называется размерностью пространства (обозначается dimV).
Связанные определения
- Линейное пространство называют конечномерным, если оно имеет конечный базис, и бесконечномерным, если оно не имеет конечного базиса.
- Представление вектора в виде (конечной) линейной комбинации базисных векторов называется разложением вектора по данному базису Гамеля.
Примеры
- Векторы
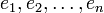 пространства
пространства  образуют базис тогда и только тогда, когда определитель матрицы, составленной из координатных столбцов этих векторов, не равен 0:
образуют базис тогда и только тогда, когда определитель матрицы, составленной из координатных столбцов этих векторов, не равен 0: 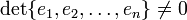 .
. - В пространстве всех многочленов над полем один из базисов составляют степенные функции:
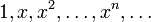 .
. - Понятие базиса используется в бесконечномерном случае, например вещественные числа образуют линейное пространство над рациональными числами и оно имеет континуальный базис Гамеля и, соответственно, континуальную размерность.
Базис Ша́удера
Система векторов {en} топологического векторного пространства L называется базисом Шаудера (англ. Shauder basis), если каждый элемент
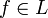 разлагается в единственный, сходящийся к f ряд по {en}:
разлагается в единственный, сходящийся к f ряд по {en}:где fi — числа, называемые коэффициентами разложения вектора f по базису {en}.
Чтобы подчеркнуть отличие определения базиса Гамеля для общих линейных пространств (допускаются только конечные суммы) от базиса Шаудера для топологических векторных пространств (допускается разложение в сходящийся ряд) для первого часто используют термин линейный базис, оставляя термин базис для разложений в ряды. Мощность линейного базиса называют также линейной размерностью. В конечномерных пространствах эти определения совпадают из-за конечности базиса. В бесконечномерных пространствах эти определения существенно различаются и линейная размерность может быть строго больше мощности базиса Шаудера.
Например, никакое бесконечномерное Гильбертово пространство не имеет счетного линейного базиса, хотя может иметь счетные базисы Шаудера с разложением в ряд, в том числе, ортонормированные базисы. Все ортонормированные базисы Гильбертовых пространств являются базисами Шаудера, например, множество функций
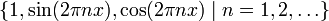 является базисом Шаудера в пространстве L2[0,1]. В более общих банаховых пространствах понятие ортонормированного базиса неприменимо, но часто удаётся построить базисы Шаудера, не использующие ортогональности.
является базисом Шаудера в пространстве L2[0,1]. В более общих банаховых пространствах понятие ортонормированного базиса неприменимо, но часто удаётся построить базисы Шаудера, не использующие ортогональности.Пример: базис Шаудера для пространства непрерывных функций C[a,b]
C[a,b] — банахово пространство с нормой
![\|f\| = \max_{x \in [a,b]}|f(x)|](/pictures/wiki/files/54/6eb586a8e3e85bcb7c1362ff99d163e4.png) . Для разложений в ряды Фурье и обобщенные ряды Фурье по ортонормированным системам функций легко доказывается сходимость в Гильбертовом пространстве L2[a,b], но не в C[a,b]. Шаудер сконструировал базис Шаудера {en} для C[a,b]. Пусть
. Для разложений в ряды Фурье и обобщенные ряды Фурье по ортонормированным системам функций легко доказывается сходимость в Гильбертовом пространстве L2[a,b], но не в C[a,b]. Шаудер сконструировал базис Шаудера {en} для C[a,b]. Пусть 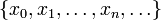 — плотное счетное множество точек на [a,b], x0 = a, x1 = b, остальные точки могут быть, например, всеми рациональными точками отрезка [a,b], упорядоченными произвольным образом. Положим: e0 = 1, e1 = (x − a) / (b − a) — линейная функция. Определим кусочно-линейную функцию en(x) так, чтобы en(xi) = 0 при
— плотное счетное множество точек на [a,b], x0 = a, x1 = b, остальные точки могут быть, например, всеми рациональными точками отрезка [a,b], упорядоченными произвольным образом. Положим: e0 = 1, e1 = (x − a) / (b − a) — линейная функция. Определим кусочно-линейную функцию en(x) так, чтобы en(xi) = 0 при 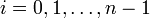 и en(xn) = 1. Точки
и en(xn) = 1. Точки 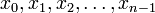 разбивают [a,b] на n − 1 отрезок. Точка xn лежит строго внутри одного из них. Пусть это In = [xj,xk] для каких-то
разбивают [a,b] на n − 1 отрезок. Точка xn лежит строго внутри одного из них. Пусть это In = [xj,xk] для каких-то 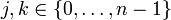 (порядок нумерации чисел
(порядок нумерации чисел 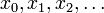 не соответствует их величине).
не соответствует их величине).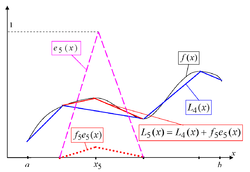 Разложение непрерывной функции по базису Шаудера. Показано построение L5(x). Красным цветом на графике выделен участок, на котором L5 отличается от L4 (синяя ломаная).
Разложение непрерывной функции по базису Шаудера. Показано построение L5(x). Красным цветом на графике выделен участок, на котором L5 отличается от L4 (синяя ломаная).Положим:
- en(x) = 0 вне отрезка In = [xj,xk],
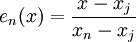 при
при ![x \in [x_j,x_n],](/pictures/wiki/files/98/bc4936f49e333b7ddf74a60239a4a7c2.png)
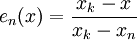 при
при ![x \in [x_n,x_k].](/pictures/wiki/files/50/22c81cba5df166a509cb6f4a7f700e0d.png)
Полученная система кусочно-линейных «шапочек» и есть искомый базис Шаудера. Коэффициенты разложения произвольной функции
![f(x) \in C[a,b]](/pictures/wiki/files/49/1f94c1a52ec747742f1ae857b5b43fbf.png) по этому базису выражаются по явным реккурентным формулам через последовательность значений f(xi). Частичная сумма первых n + 1 членов ряда
по этому базису выражаются по явным реккурентным формулам через последовательность значений f(xi). Частичная сумма первых n + 1 членов рядаявляется в данном случае кусочно-линейной аппроксимацией f(x) с узлами в точках
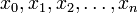 ; формула для коэффициентов
; формула для коэффициентов 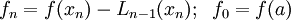 (см. Рис.)
(см. Рис.)Проблема базиса
Базисы Шаудера построены для большинства известных примеров банаховых пространств, однако проблема Банаха — Шаудера о существовании базиса Шаудера в каждом сепарабельном банаховом пространстве не поддавалась решению более 50 лет и лишь в 1972 году была решена отрицательно: существуют сепарабельные банаховы пространства без базиса Шаудера (контрпримеры Энфло, Шанковского, Дэви и Фигеля).
См. также
- Репер — близкое понятие для аффинного пространства.
- Ортогональный базис — специальный класс базисов (базисов Шаудера) для пространств со скалярным произведением (Гильбертово пространство).
- Базис Грёбнера
Литература
- Кутателадзе С. С., Основы функционального анализа. — 4 изд., испр. — Новосибирск: Изд-во Ин-та Математики СО РАН, 2001. — XII+354 c.
Wikimedia Foundation. 2010.