- Задача о независимом наборе
-
Задача о независимом множестве относится к классу NP-полных задач в области теории графов. По сути, она полностью эквивалентна задаче о клике.
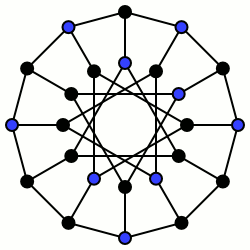 Независимый набор из 9 голубых вершин
Независимый набор из 9 голубых вершинМножество вершин графа называется независимым, если никакие две вершины этого множества не соединены ребром. Другими словами, индуцированный этим множеством подграф состоит из изолированных вершин. Иногда также говорят, что каждое ребро графа инцидентно не более чем одной вершине из независимого множества. Задача разрешения выглядит так: существует ли в заданном графе G независимое множество размера k? Соответствующая ей оптимизационная задача, она же задача о независимом множестве, формулируется следующим образом: в заданном графе G требуется найти независимое множество максимального размера.
Иногда эту задачу называют поиском независимого множества максимального размера или максимального (по размеру) независимого множества. Не стоит путать это понятие с максимальным (по включению) независимым множеством, которое определяется как такое независимое множество вершин, что при добавлении к нему еще одной (любой) вершины исходного графа оно перестает быть независимым. Понятно, что таких множеств, вообще говоря, может быть несколько и разных размеров. Максимальное по включению независимое множество отнюдь не всегда является максимальным по размеру. В то же время, каждое независимое множество максимального размера по определению является также и максимальным по включению. Для нахождения (какого-то) максимального по включению независимого множества можно воспользоваться жадным алгоритмом, работающим за полиномиальное время, тогда как задача о независимом множестве максимального размера принадлежит к классу NP-полных задач.
Содержание
Максимальное независимое множество в дереве
Если данный граф является деревом, то задача о независимом множестве эффективно решается методом динамического программирования.
Оптимальная подструктура задачи
Структура дерева сама подсказывает решение задачи: Обозначим корнем дерева любую вершину и назовем её r. Обозначим через
I(u)размер максимального независимого множества дерева, корнем которого является вершина u. Ответом на задачу будет являтьсяI(r). Опишем формально решение задачи:I(u)= max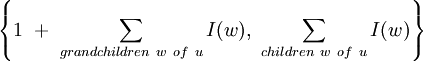
grandchildren обозначает «внуков» вершины(то есть детей их детей), а children обозначает детей вершины. Формула объясняется просто: Если мы включаем вершину u в максимальное независимое множество, то его мощность увеличивается на 1, но его детей мы брать не можем(так как они соединены ребром с вершиной u), если же мы не включаем её, то мощность максимального независимого множества будет равен сумме размеров независимых множеств детей этой вершины. Остается только выбрать максимум из этих двух вариантов, чтобы получить решение задачи.
Псевдокод
Считаем что в вершине u хранится
I(u):function get_independent_set(Node u) { если I(u) уже посчитано, то возвратить I(u) //мощность множества, которое можно получить, если не брать вершину u children_sum = 0 //мощность множества, которое можно получить, если взять вершину u grandchildren_sum = 0 //цикл по всем детям for i := 1 to child_num do children_sum = children_sum + get_independent_set(children[i]) //цикл по всем внукам for i:= 1 to grandchildren_num grandchildren_sum = grandchildren_sum + get_independent_set(grandchildren[i]) //запоминаем, чтобы не персчитывать ещё раз I(u) = max(1 + grandchildren_sum, children_sum) возвратить I(u) }Вызов get_independent_set(r) даст ответ на задачу, где r — корень дерева(любая выбранная вершина в нашем случае). Время выполнения алгоритма, очевидно, O(|V| + |E|).
Литература
- Chris Godsil Algebraic Graph Theory. — New York: Springer, 2004. — ISBN 0-387-95220-9
- Richard Karp. Reducibility Among Combinatorial Problems. Proceedings of a Symposium on the Complexity of Computer Computations. 1972.
- Computers and Intractability: A Guide to the Theory of NP-Completeness. — W.H. Freeman, 1979. — ISBN ISBN 0-7167-1045-5 A1.2: GT20, pg.194.
- Moon, J. W. & Moser, L. (1965), "On cliques in graphs", Israel J. Math. 3: 23–28, MR0182577
- Sanjoy Dasgupta , Christos H. Papadimitriou, Umesh Vazirani Algorithms. — 1-е изд. — McGraw-Hill Science/Engineering/Math, 2006. — С. 336. — ISBN 0073523402
Примечания
См. также
Алгоритм Брона — Кербоша - быстрое нахождение максимальных (по включению) независимых множеств вершин
Ссылки
- Weisstein, Eric W. Maximal Independent Vertex Set на сайте Wolfram MathWorld.(англ.)
- Challenging Benchmarks for Maximum Clique, Maximum Independent Set, Minimum Vertex Cover and Vertex Coloring
- Статья о методах решения труднорешаемых задач
- Слайды лекции о динамическом программировании
NP-полные (трудные) задачи Теория сложности вычислений Упаковка, укладка Упаковка в контейнеры: двумерная упаковка • линейная упаковка • упаковка по весу • упаковка по стоимости
Задача о ранце (рюкзаке)Булева формула Задача выполнимости булевых формул Коммивояжёр Задача коммивояжёра Вершинное покрытие Задача о вершинном покрытии Клика Задача о клике Независимое множество Задача о независимом множестве (наборе) Покрытие множества Задача о покрытии множества Латинский квадрат Задача о заполнении латинского квадрата Обобщённое судоку Задача обобщённого судоку Какуро Задача какуро Пятнашки (обобщённые) Задача поиска кратчайшего решения (костяшек более 15) Классы сложности
Wikimedia Foundation. 2010.
