- Задача о рюкзаке
-
Задача о ранце (рюкзаке) — одна из задач комбинаторной оптимизации. Название это получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов ограничен. Подобные задачи часто возникают в экономике, прикладной математике, криптографии. В общем виде, задачу можно сформулировать так: из неограниченного множества предметов со свойствами «стоимость» и «вес», требуется отобрать некое число предметов таким образом, чтобы получить максимальную суммарную стоимость при одновременном соблюдении ограничения на суммарный вес.
Содержание
Разновидности
- Каждый предмет из множества можно выбирать бесконечное количество раз.
- Каждый предмет можно использовать только один раз.
Решение
Задача о ранце в случае, когда вес каждого предмета представляет собой целое число, может быть решена с помощью динамического программирования. Но важно отметить, что задача о ранце является NP-задачей (псевдо-полиномиальна).
Задача о ранце с возможностью бесконечного выбора предметов
Формулировка
По данному набору из n предметов стоимостями v1,v2,...,vn и весами w1,w2,...,wn найти поднабор (с учетом того, что можно брать один предмет несколько раз), такой что его стоимость будет максимальна, среди всех поднаборов веса не более W.
Решение
Обозначим через Kw максимальную стоимость, которую мы можем набрать при весе не более w. Получаем следующее рекуррентное соотношение:
- K0 = 0 (при весе не более нуля максимальная стоимость 0)
- Kw = max {
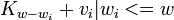 , 1 <= i <= n, где n - размер набора }
, 1 <= i <= n, где n - размер набора }
Использовать рекурсию напрямую нельзя, т.к. появляется большое число перекрывающихся задач и время выполнения может стать экспоненциальным. При использовании динамического программирования(запоминания) мы получаем сложность O(n * W) - псевдо-полиномиальный алгоритм.
Реализация
#include <vector> #include <limits> //wts - массив весов, cost - массив стоимостей предметов, W - вместимость рюкзака //функция возвращает максимальную стоимость, которую можно набрать(решение задачи о рюкзаке //с повторениями) //массив dp собственно реализует динамическое программирование, описанное в статье, как K_w int knapsack1(const std::vector<int>& wts, const std::vector<int>& cost, int W) { size_t n = wts.size(); std::vector<int> dp(W + 1); dp[0] = 0; for (int w = 1; w <= W; w++) { dp[w] = std::numeric_limits<int>::min(); for (size_t i = 0; i < n; i++) { if (wts[i] <= w) { dp[w] = std::max(dp[w], dp[w - wts[i]] + cost[i]); } } } return dp[W]; }
Задача о ранце с возможностью единичного выбора предмета
Решение
Обозначим через Kw,i максимальную стоимость, которую мы можем набрать при весе не более w среди i первых предметов. Получаем следующее рекуррентное соотношение:
- K0,j = 0, 0 <= j <= n
- Kw,0 = 0, 0 <= w <= W
- Kw,i = max{Kw,i − 1,
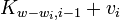 } | 0 <= w <= W, wi <= w}
} | 0 <= w <= W, wi <= w} - Kw,i = Kw,i − 1, если wi > w (не можем положить предмет данного веса)
Реализация
#include <vector> #include <limits> int knapsack2(const std::vector<int>& wts, const std::vector<int>& cost, int W) { size_t n = wts.size(); std::vector<std::vector<int> > dp(W + 1); for (int i = 0; i <= W; i++) { dp[i].resize(n + 1); dp[i][0] = 0; } for (size_t i = 0; i <= n; i++) { dp[0][i] = 0; } for (size_t j = 1; j <= n; j++) { for (int w = 1; w <= W; w++) { if (wts[j-1] <= w) { dp[w][j] = std::max(dp[w][j - 1], dp[w - wts[j-1]][j - 1] + cost[j-1]); } else { dp[w][j] = dp[w][j - 1]; } } } return dp[W][n]; }
См. также
NP-полные (трудные) задачи Теория сложности вычислений Упаковка, укладка Упаковка в контейнеры: двумерная упаковка • линейная упаковка • упаковка по весу • упаковка по стоимости
Задача о ранце (рюкзаке)Булева формула Задача выполнимости булевых формул Коммивояжёр Задача коммивояжёра Вершинное покрытие Задача о вершинном покрытии Клика Задача о клике Независимое множество Задача о независимом множестве (наборе) Покрытие множества Задача о покрытии множества Латинский квадрат Задача о заполнении латинского квадрата Обобщённое судоку Задача обобщённого судоку Какуро Задача какуро Пятнашки (обобщённые) Задача поиска кратчайшего решения (костяшек более 15) Классы сложности - Задача об упаковке в контейнеры
- Метод ветвей и границ
- Дискретное программирование
- Математическое программирование
- Оптимизация
- Исследование операций
Литература
- Ананий В. Левитин Глава 3. Метод грубой силы: Задача о рюкзаке // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Aigorithms. — М.: «Вильямс», 2006. — С. 160-163. — ISBN 0-201-74395-7
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
- Роберт Седжвик. Фундаментальные алгоритмы на C++. Части 1-4. Анализ. Структуры данных. Сортировка. Поиск = Algorithms in C++. Parts 1-4. Fundamentals. Data Structures. Sorting. Searching. — 3-е изд. — Россия, Санкт-Петербург: «ДиаСофт», 2002. — С. 688. — ISBN 5-93772-047-4, 0-201-35088-2
Wikimedia Foundation. 2010.
