Формула О'Нэйла

Риманова субмерсия — субмерсия между римановыми многообразиями, которая инфинитезимально является ортогональной проекцией.

Определение

Пусть (M,g) и (N,h) — римановы многообразия. Гладкое отображение 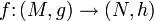$f\colon(M,g)\to (N,h)$ называется римановой субмерсией, если для любой точки x есть изометрическое линейное вложение 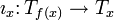$\imath_x\colon T_{f(x)}\to T_x$ такое, что 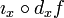$\imath_x \circ d_xf$ есть ортогональная проекция, здесь d_xf обозначает дифференциал отображения f в точке x.

Для вектора 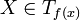$X\in T_{f(x)}$ вектор 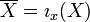$\overline{X}=\imath_x(X)$ называется горизонтальным поднятием X.

Формула О’Нэйла

Пусть 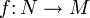$f\colon N\to M$ — риманова субмерсия. Тогда для любых векторных полей X, Y на M, значение тензора кривизны R_M можно вычислить используя формулу О’Нэйла

• $\langle R_M(X,Y)Y,X\rangle=\langle R_N(\overline{X},\overline{Y})\overline{Y},\overline{X}\rangle+\tfrac34\left|[\overline{X},\overline{Y}]^V\right|^2$,

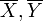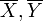где $\overline{X},\overline{Y}$ — горизонтальные поднятия полей X и Y соответственно, $[\overline{X},\overline{Y}]^V$ — вертикальная составляющая скобки Ли векторных полей $\overline{X},\overline{Y}$ на N.

Следствия

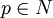• Абсолютная величина $[\overline{X},\overline{Y}]^V$ в точке $p\in N$ зависит только от точки p и значений X и Y в точке f(p).
• Если тотальное пространство римановой субмерсии имеет секционную кривизну 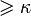$\geqslant\kappa$, то то же верно и для базы.

Вариации и обобщения

• Субметрия — 1-липшицево и 1-колипшицево отображение между метрическими пространствами.