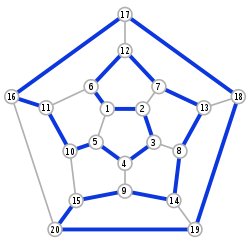
- Гамильтонов граф
-
 Гамильтонов путь (чёрным)
Гамильтонов путь (чёрным)Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл.
Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом (см. Словарь терминов теории графов). Задача определения содержит ли данный граф гамильтонов цикл является NP-полной.
Гамильтоновы путь, цикл и граф названы в честь ирландского математика У. Гамильтона, который впервые определил эти классы, исследовав задачу «кругосветного путешествия» по додекаэдру, узловые вершины которого символизировали крупнейшие города Земли, а рёбра — соединяющие их дороги.
Содержание
Условия существования
Необходимое условие
Если неориентированный граф G содержит гамильтонов цикл, тогда в нём не существует ни одной вершины x(i) с локальной степенью p(x(i)) < 2. Доказательство следует из определения.
Условие Дирака (англ.) (1952)
Пусть
 — число вершин в данном графе; если степень каждой вершины не меньше, чем
— число вершин в данном графе; если степень каждой вершины не меньше, чем  , то граф называется графом Дирака. Граф Дирака — гамильтонов.
, то граф называется графом Дирака. Граф Дирака — гамильтонов.Условие Оре (1960)
Пусть
 — количество вершин в данном графе. Если для любой пары несмежных вершин
— количество вершин в данном графе. Если для любой пары несмежных вершин  выполнено неравенство
выполнено неравенство  , то граф называется графом Оре (словами: степени любых двух несмежных вершин не меньше общего числа вершин в графе). Граф Оре — гамильтонов.
, то граф называется графом Оре (словами: степени любых двух несмежных вершин не меньше общего числа вершин в графе). Граф Оре — гамильтонов.Теорема Бонди-Хватала
Теорема Бонди-Хватала (англ.) обобщает утверждения Дирака и Оре. Для графа G с n вершинами замыкание определяется добавлением в G ребра (u,v) для каждой пары несмежных вершин u и v, сумма степеней которых не меньше n.
Граф является гамильтоновым тогда и только тогда, когда его замыкание — гамильтонов граф.
Условие Поша
Введем следующую функцию
 целого неотрицательного аргумента
целого неотрицательного аргумента  на графе
на графе ![G = [A, B]](15312e95170d7f5fa2b6c250cb2a57f0.png) :
: .
.
Написанное означает, что функция
 в каждом целом неотрицательном
в каждом целом неотрицательном  принимает значение, равное количеству вершин графа
принимает значение, равное количеству вершин графа ![G = [A, B]](15312e95170d7f5fa2b6c250cb2a57f0.png) , степень которых не превосходит
, степень которых не превосходит  . Такую функцию
. Такую функцию  называют функцией Поша графа
называют функцией Поша графа  .
.См. также
- Эйлеров цикл
- Задача коммивояжёра
- Задача о ходе коня
- Проблема семи мостов Кёнигсберга
- Китайская стена (головоломка)
Ссылки
- Weisstein, Eric W. Hamiltonian Circuit (англ.) на сайте Wolfram MathWorld.
- Теория графов и комбинаторика
- Видеолекция посвященная Эйлеровым и Гамильтоновым графам
- Эйлеровы и Гамильтоновы графы
Категория:- Теория графов
Wikimedia Foundation. 2010.