Граф Мура

Граф Петерсена

Граф Хивуда

Граф Макджи

Граф Леви

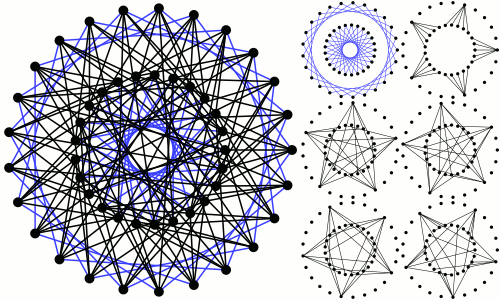Граф Гофмана-Синглтона

n-клетка — кубический граф обхвата n с наименьшим возможным числом вершин. для каждого 2 < n < 9 существует единственная n-клетка, причем все эти графы обладают высокой симметрией (являются унитранзитивными). Кроме того, при изображении на плоскости они часто дают экстремальное количество самопересечений, далее индекс самопересечения см. [1]

• 3-клетка - К₄, остов тетраэдра, 4 вершины.
• 4-клетка — К_3,3, один из двух минимальных не планарных графов, 6 вершин.
• 5-клетка — Граф Петерсена, 10 вершин. Минимальный кубический граф с индексом самопересечения 2.
• 6-клетка — Граф Хивуда, 14 вершин. Разбивается на 1-факторы (то есть, реберно раскрашиваем), любая сумма двух факторов образует гамильтонов цикл. Минимальный кубический граф с индексом самопересечения 3.
• 7-клетка — Граф Макджи, 24 вершины. Минимальный кубический граф с индексом самопересечения 8.
• 8-клетка — Граф Леви, 30 вершин.

Обобщенное определение

(r,n)-клетка — регулярный граф степени r и обхвата n с наименьшим возможным числом вершин.

Тривиальные семейства

• (2,n)-клетками являются, очевидно, циклические графы C_n;
• (r-1,3)-клетки — полные графы К_r;
• (2r,4)-клетки — полные графы К_r,r;

Не тривиальные представители

• (7,5)-клетка — Граф Гофмана-Синглтона, 50 вершин.

Известны еще некоторые клетки. В таблице ниже показано количество вершин в (r,n)-клетках степени 8 > r > 2 и обхвата 13 > n > 2. Клетки для этих и больших r и n описаны тут ^[1].

n:	3	4	5	6	7	8	9	10	11	12
r = 3:	4	6	10	14	24	30	58	70	112	126
r = 4:	5	8	19	26	67	80	275	384		728
r = 5:	6	10	30	42	152	170				2730
r = 6:	7	12	40	62	294	312				7812
r = 7:	8	14	50	90

Графы Мура

Количество вершин в (r,n)-клетке больше или равно

$1+r\sum_{i=0}^{(n-3)/2}(r-1)^i$ для нечетных n и

$2\sum_{i=0}^{(n-2)/2}(r-1)^i$ для четных.

Если имеет место равенство, то соответствующий граф называется графом Мура. В то время как клетка существует для всяких r > 2 и n > 2, нетривиальных графов Мура гораздо меньше. Из вышеупомянутых клеток, графами Мура являются Граф Петерсена, граф Хивуда, граф Леви и граф Гофмана-Синглтона. Доказано,^[2][3][4] что все нечетные случаи исчерпываются n = 5, r = 2, 3, 7 и, возможно, 57, а четные n = 6, 8, 12.

Примечания

1. ↑ http://people.csse.uwa.edu.au/gordon/cages/allcages.html (англ.)
2. ↑ Bannai, E. and Ito, T. "On Moore Graphs." J. Fac. Sci. Univ. Tokyo Ser. A 20, 191-208, 1973
3. ↑ Damerell, R. M. "On Moore Graphs." Proc. Cambridge Philos. Soc. 74, 227-236, 1973
4. ↑ Hoffman, A. J. and Singleton, R. R. "On Moore Graphs of Diameter 2 and 3." IBM J. Res. Develop. 4, 497-504, 1960

Литература

• Ф. Харари Теория графов. — М.: УРСС, — 2003. — 300 с — ISBN 5-354-00301-6.

Ссылки

http://mathworld.wolfram.com/CageGraph.html (англ.)

http://people.csse.uwa.edu.au/gordon/cages/ (англ.)