Фигурные числа

Фигу́рные чи́сла — общее название чисел, связанных с той или иной геометрической фигурой. Это историческое понятие восходит к пифагорейцам. Предположительно от фигурных чисел возникло выражение: «Возвести число в квадрат или в куб».

Виды фигурных чисел

Различают следующие виды фигурных чисел:

• Линейные числа — числа, не разлагающиеся на сомножители, то есть их ряд совпадает с рядом простых чисел, дополненным единицей:

  1, 2, 3, 5, 7, 11, 13, 17, 19, 23, … (последовательность A008578 в OEIS)

• Плоские числа — числа, представимые в виде произведения двух сомножителей, то есть составные:

  4, 6, 8, 9, 10, 12, 14, 15, … (последовательность A002808 в OEIS)

• Телесные числа — числа, представимые произведением трёх сомножителей:

  8, 12, 16, 18, 20, 24, 27, 28, … (последовательность A033942 в OEIS)

• Многоугольные числа

Многоугольные числа

n-е по порядку m-угольное число $P_n$ можно определить как сумму n членов арифметической прогрессии, у которой первый член есть 1, а разность равна $m-2$. Например, треугольные числа получаются как частичные суммы ряда $1+2+3+4 \dots$.

Треугольные числа

Основная статья: Треугольное число

Последовательность треугольных чисел:

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, 1326, 1378, 1431, …, $\frac{n(n+1)}{2}$, … (последовательность A000217 в OEIS)

Свойства:

• Сумма двух последовательных треугольных чисел даёт полный квадрат (квадратное число).
• Чётность элемента последовательности меняется с периодом 4: нечётное, нечётное, чётное, чётное.

Квадратные числа

Основная статья: Квадратное число

1	4	9

Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, …, n², … (последовательность A000290 в OEIS)

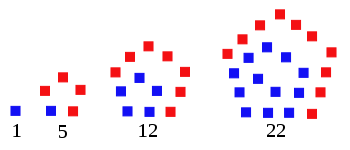
Пятиугольные числа

1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162, 1247, 1335, 1426, 1520, 1617, 1717, 1820, 1926, 2035, 2147, 2262, 2380, 2501, 2625, 2752, 2882, 3015, 3151, …, $\frac{n(3n-1)}{2}$, … (последовательность A000326 в OEIS)

Шестиугольные числа

Основная статья: Шестиугольное число

1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780, 861, 946, 1035, 1128, 1225, 1326, 1431, 1540, 1653, 1770, 1891, 2016, 2145, 2278, 2415, 2556, 2701, 2850, 3003, 3160, 3321, 3486, 3655, 3828, 4005, 4186, 4371, 4560 …, $2n^2-n$, … (последовательность A000384 в OEIS)

Общий случай

Последовательность k-угольных чисел:

1, k, 3k-3, 6k-8, 10k-15, 15k-24, 21k-35, 28k-48, 36k-63, 45k-80, …, $n + (k - 2)\frac{n(n-1)}{2}$, …

Эквивалентный формат представления n-го элемента: $\frac{n((k - 2)(n-1)+2)}{2}$.

Многомерные фигурные числа

Можно определить многомерные фигурные числа,^{[источник не указан 666 дней]} частными случаями которых являются:

• Изоэдральные многомерные фигурные числа. Пример: последовательность A081436 в OEIS.

• Элементарные многомерные фигурные числа:
  • Гиперкубические: $A^k_n=n^k$
  • Симплексные: $P^k_n=\tbinom{n-1+k}{k}=\tfrac{(n-1+k)!}{(n-1)!k!}$. В частности, $P^2_n$ — это треугольные числа, $P^3_n$ — тетраэдрические числа.
  • Гипероктаэдрные: $T^k_n=T^{k-1}_n+T^k_{n-1}+T^{k-1}_{n-1}$, где $T^1_n=n$. Пример: последовательность A014820 в OEIS.

• Трехмерные правильные фигурные числа:

  $P^3_n=n+(e-2)\frac{n(n-1)}{2}+(f-m)(k-2)\frac{n(n-1)(n-2)}{6},$

где e — число вершин многогранника, f — число его граней, k — число сторон каждой грани, m — число граней, примыкающих к каждой вершине. Примеры: последовательности A006566, A006564, A005900.

• Четырехмерные правильные фигурные числа:

  $P^4_n=n+(E-2)\frac{n(n-1)}{2}+(G-\frac{m_f}{2})(f-m)(k-2)\frac{n(n-1)(n-2)}{6}+(G-m_f)(f-m)(k-2)\frac{n(n-1)(n-2)(n-3)}{24},$

где E — число вершин, G — число граней $m_f$ — число многогранных углов вершины. Примеры: последовательности A092182, A092181, A092183.

Исторический очерк

Фигурные числа, по мнению пифагорейцев, играют важную роль в структуре мироздания. Поэтому их изучением занимались многие математики античности: Эратосфен, Гипсикл, Диофант Александрийский и другие. Гипсикл (II век до н. э.) дал общее определение m-угольного числа $P_n$ как суммы n членов арифметической прогрессии, у которой первый член есть 1, а разность равна $m-2$. Диофант написал большое исследование о свойствах многоугольных чисел, фрагменты которого дошли до наших дней. О фигурных числах много говорится в пифагорейских учебниках арифметики, созданных Никомахом Геразским и Теоном Смирнским (II век), установившие ряд зависимостей между фигурными числами разных размерностей. Большой интерес к фигурным числам проявили индийские математики и первые математики средневековой Европы (Фибоначчи, Пачоли, Кардано и др.).

В Новое время многоугольными числами занимались Ферма, Валлис, Эйлер, Лагранж, Гаусс и другие. Ферма сформулировал (1637) так называемую «золотую теорему»:

• Всякое натуральное число — либо треугольное, либо сумма двух или трёх треугольных чисел;
• Всякое натуральное число — либо квадратное, либо сумма двух, трёх или четырёх квадратных чисел (Теорема Лагранжа о сумме четырёх квадратов);
• Всякое натуральное число — либо пятиугольное, либо сумма от двух до пяти пятиугольных чисел:
• и т. д.

Этой теоремой занимались многие выдающиеся математики, полное доказательство сумел дать Коши в 1813 году.^[1]

См. также

• Последовательность

Примечания

1. ↑ Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975. — С. 10-11. — 208 с.

Литература

• Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.
• Депман И. Я. История арифметики. Пособие для учителей. — Изд.второе. — М.: Просвещение, 1965. — С. 150—155.
• Матвиевская Г. П. Заметки о многоугольных числах в записных книжках Эйлера // Историко-математические исследования. — М.: Наука, 1983. — № 27. — С. 27-49.
• Серпинский В. Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.
• Стиллвелл Д. Глава 3 // Математика и ее история. — Москва-Ижевск: Институт компьютерных исследований, 2004.