Кошмар Фубини

Кошмар Фубини (англ. Fubini Nightmare) — название кажущегося нарушения теоремы Фубини в не-абсолютно непрерывных слоениях с гладкими слоями. Состоит в том, что множество в расслоенном пространстве, пересекающее все слои по множеству меры ноль (или даже вообще по отдельным точкам), может, тем не менее, иметь положительную (и даже полную!) меру в объемлющем пространстве. Такой эффект, на самом деле, теореме Фубини не противоречит, поскольку выпрямляющее отображение слоения не является абсолютно непрерывным.

Существование «кошмара Фубини» затрудняет проведение доказательств для частично-гиперболических динамических систем «послойно» по слоям центрального слоения: это слоение обычно лишь гёльдерово, но не абсолютно непрерывно.

Иллюстративная версия кошмара Фубини была придумана А. Катком и опубликована Дж. Милнором в работе «Fubini foiled: Katok’s paradoxical example in measure theory», а в 2000 году динамическая реализация такого примера была построена для случая центрального слоения в работе Э. Вилкинсон и М. Шуба «Pathological foliations and removable zero exponents».

Конструкция Катка

Слоение

Для любого p, 0<p<1, можно рассмотреть кодирование точек отрезка [0,1] последовательностями нулей и единиц, с делением очередного отрезка в отношении $(1-p):p$. (Как и при обычном кодировании, при этом будет иметь место отождествление 0 с хвостом из единиц и 1 с хвостом из нулей.)

Точка, кодирующаяся данной последовательностью $(a_1, a_2, ...) \in \{0,1\}^{\N},$, может быть несложно задана явно: отрезок, полученный после первых n делений, имеет длину $l_n= p^{\# \{j\le n: a_j=1\}} (1-p)^{\# \{j\le n: a_j=0\}},$ поэтому соответствующая точка равна $F_p(a_1,a_2,\dots) = \sum_{n: a_n=1} a_n (1-p) l_{n-1} = \sum_{n=1}^{\infty} a_n p^{\# \{j\le n-1: \, a_j=1\}} (1-p)^{1+\,\# \{j\le n-1: \, a_j=0\}}.$

Слоение Катка

Для фиксированной последовательности $a \in \{0,1\}^{\N}$ отображение $p\mapsto F_p(a)$ аналитично. (Проще всего это следует из теоремы Вейерштрасса и того факта, что задающий его ряд сходится равномерно на компактах внутри пересечения кругов $\{|p| <1 \} \cap \{|1-p| <1 \} \subset \mathbb{C}$.)

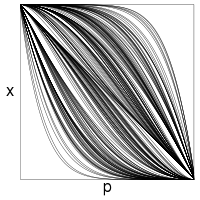
Поэтому разбиение квадрата $(0,1)\times [0,1]$ на графики по переменной p отображений $F_p(a)$ — кривые $\gamma_a = \{ (p, F_p(a)) \mid p\in (0,1) \}$, с параметром a, пробегающим $\{0,1\}^{\N}$, — слоение на аналитические кривые.

Множество

При любом фиксированном p, цифры $a_1=\xi_1(x;p), a_2=\xi_2(x;p)$, … кодирования случайной (выбираемой в соответствии с мерой Лебега) точки $x\in [0,1]$ — независимые бернуллевские случайные величины, принимающие значение 1 с вероятностью p и 0 с вероятностью 1-p.

В силу закона больших чисел, при любом p для почти всех x выполнено

$\frac{1}{n} \sum_{j=1}^n a_j(x;p) \to p, \quad n\to\infty.$

Из теоремы Фубини тогда вытекает, что множество

$M:= \left\{ (p,x) \mid \frac{1}{n} \sum_{j=1}^n a_j(x;p) \xrightarrow[n\to\infty]{} p. \right\}$

имеет полную меру Лебега в квадрате $(0,1)\times [0,1]$.

Однако для любой фиксированной последовательности $(a_i)$ предел её чезаровских средних, если он существует, единственен. Поэтому любая кривая $\gamma_a$ либо вообще не пересекает множество M (если предела нет), либо пересекает в единственной точке (p,F_p(a)), где

$p=\lim_{n\to\infty} \frac{a_1+\dots+ a_n}{n}.$

Таким образом, для построенных слоения и множества M имеет место «кошмар Фубини».

Конструкция Вилкинсон — Шуба

Вилкинсон и Шуб рассматривали диффеоморфизмы, являющиеся малыми возмущениями диффеоморфизма $A\times id$ трёхмерного тора $T^3=T^2\times S^1$, где $A=\left(\begin{smallmatrix} 2& 1 \\ 1 &1\end{smallmatrix}\right):T^2\to T^2$ — диффеоморфизм Аносова. Это отображение, а, значит, и близкие к нему частично гиперболичны. Более того, центральные слои возмущённых отображений будут являться гладкими окружностями, близкими к исходным.

Возмущение Вилкинсон — Шуба, которое берётся в классе сохраняющих меру Лебега отображений, делало диффеоморфизм эргодичным, но при этом центральный показатель Ляпунова становился ненулевым. С точностью до обращения, его можно считать положительным. Тогда множество точек, центральный показатель Ляпунова для которых положителен, имеет в $T^3$ полную меру Лебега.

С другой стороны, центральные слои-окружности имеют ограниченную сверху длину, поэтому на каждой из них множество точек, в которых происходит растяжение в центральном направлении, обязано иметь меру ноль. Более тонкие рассуждения показывают, что, более того, это множество обязано состоять из конечного числа точек, то есть имеет место «кошмар Фубини».

Литература

• J. Milnor, Fubini foiled: Katok’s paradoxical example in measure theory. Math. Intelligencer 19 (1997), no. 2, 30—32.
• M. Shub, A. Wilkinson, Pathological foliations and removable zero exponents, Invent. math. 139 (2000), 495—508.